
分析 先根据ab>0,$\frac{a}{c}$<0得出a、b同号,a、c异号,那么$\frac{a}{b}$>0,$\frac{c}{b}$<0,再根据一次函数的图象与系数的关系进行解答即可.
解答 解:∵ab>0,$\frac{a}{c}$<0,
∵a、b同号,a、c异号,
∴b、c异号,
∴$\frac{a}{b}$>0,$\frac{c}{b}$<0,
∴y=$\frac{a}{b}$x+$\frac{c}{b}$过一、三、四象限.
∴这条直线不经过第二象限,
故答案为:二.
点评 本题考查的是一次函数的图象与系数的关系,解答此题的关键是根据ab>0,ac<0得出$\frac{a}{b}$>0,$\frac{c}{b}$<0.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:选择题
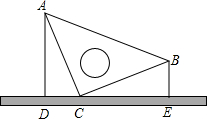 如图,桌面上竖直放置一等腰直角三角板ABC,若测得斜边AB在桌面上的投影DE为8cm,且点B距离桌面的高度为3cm,则点A距离桌面的高度为( )
如图,桌面上竖直放置一等腰直角三角板ABC,若测得斜边AB在桌面上的投影DE为8cm,且点B距离桌面的高度为3cm,则点A距离桌面的高度为( )| A. | 6.5cm | B. | 5cm | C. | 9.5cm | D. | 11cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
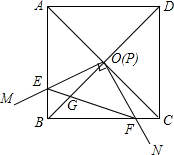 如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,∠MPN为直角,使点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM,PN分别交AB,BC于E,F两点,连接EF交OB于点G,则下列结论:①EF=$\sqrt{2}$OE;②S四边形OEBF:S正方形ABCD=1:4;③BE+BF=$\sqrt{2}$OA;④在旋转过程中,当△BEF与△COF的面积之和最大时,AE=$\frac{3}{4}$;⑤OG•BD=AE2+CF2.其中结论正确的个数是( )
如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,∠MPN为直角,使点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM,PN分别交AB,BC于E,F两点,连接EF交OB于点G,则下列结论:①EF=$\sqrt{2}$OE;②S四边形OEBF:S正方形ABCD=1:4;③BE+BF=$\sqrt{2}$OA;④在旋转过程中,当△BEF与△COF的面积之和最大时,AE=$\frac{3}{4}$;⑤OG•BD=AE2+CF2.其中结论正确的个数是( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{x+1}{x-y}$=$\frac{-x+1}{x-y}$ | B. | $\frac{{x}^{2}+{y}^{2}}{x+y}$=x+y | ||
| C. | $\frac{0.5a+b}{0.2a-0.3b}$=$\frac{5a+10b}{2a-3b}$ | D. | $\frac{a-b}{a+b}$=$\frac{b-a}{b+a}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一定是七次 | B. | 一定是四次 | C. | 一定是三次 | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com