
【题目】如图,四边形ABCD为菱形,E为对角线AC上的一个动点,连结DE并延长交射线AB于点F,连结BE.
(1)求证:∠AFD=∠EBC;
(2)若∠DAB=90°,当△BEF为等腰三角形时,求∠EFB的度数.

【答案】(1)见解析;(2) ∠EFB=30°或120°.
【解析】
(1)直接利用全等三角形的判定方法得出△DCE≌△BCE(SAS),即可得出答案;
(2)利用正方形的性质结合等腰三角形的性质得出:①当F在AB延长线上时;②当F在线段AB上时;分别求出即可.
(1)证明:∵四边形ABCD是菱形,
∴CD=AB,∠ACD=∠ACB,
在△DCE和△BCE中
 ,
,
∴△DCE≌△BCE(SAS),
∴∠CDE=∠CBE,
∵CD∥AB,
∴∠CDE=∠AFD,
∴∠EBC=∠AFD.
(2)分两种情况,
①如图1,当F在AB延长线上时,

∵∠EBF为钝角,
∴只能是BE=BF,设∠BEF=∠BFE=x°,
可通过三角形内角形为180°得:90+x+x+x=180,
解得:x=30,
∴∠EFB=30°.
②如图2,当F在线段AB上时,

∵∠EFB为钝角,
∴只能是FE=FB,设∠BEF=∠EBF=x°,则有∠AFD=2x°,
可证得:∠AFD=∠FDC=∠CBE,
得x+2x=90,
解得:x=30,
∴∠EFB=120°.
综上:∠EFB=30°或120°.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的高线,在BC边上截取点E,使得CE=BD,过E作EF∥AB,过C作CP⊥BC交EF于点P。过B作BM⊥AC于M,连接EM、PM。
(1)依题意补全图形;
(2)若AD=DC,探究EM与PM的数量关系与位置关系,并加以证明。

查看答案和解析>>
科目:初中数学 来源: 题型:
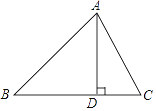
【题目】在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
某学习小组经过合作交流,给出了下面的解题思路:
作AD⊥BC于D,设BD=x,用含x的代数式表示CD→根据勾股定理,利用AD作为“桥梁”,列出方程求出x→再求出AD的长,从而计算三角形的面积.请你按照他们的解题思路完成解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①∠OBE=![]() ∠ADO;②EG=EF;③GF平分∠AGE;④EF⊥GE,其中正确的是_____.
∠ADO;②EG=EF;③GF平分∠AGE;④EF⊥GE,其中正确的是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,反映的是九(1)班学生外出乘车、步行、骑车的人数直方图的一部分和圆形分布图,下列说法:①九(1)班外出步行有8人;②在圆形统计图中,步行人数所占的圆心角度数为82°;
③九(1)班外出的学生共有40人;④若该校九年级外出的学生共有500人,那么估计全年级外出骑车的人约有150人,其中正确的结论是( )


A. ①②③ B. ①③④ C. ②③ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
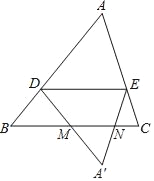
【题目】如图,在△ABC中,点D在边AB上(不与A,B重合),DE∥BC交AC于点E,将△ADE沿直线DE翻折,得到△A′DE,直线DA′,EA′分别交直线BC于点M,N.
(1)求证:DB=DM.
(2)若![]() =2,DE=6,求线段MN的长.
=2,DE=6,求线段MN的长.
(3)若![]() =n(n≠1),DE=a,则线段MN的长为 (用含n的代数式表示).
=n(n≠1),DE=a,则线段MN的长为 (用含n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学计划购进甲、乙两种规格的书柜.调查发现,若购买甲种书柜3个,乙种书柜2个,共需资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.
(1)甲、乙两种书柜每个的价格分别是多少元?
(2)若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请设计几种购买方案供这个学校选择,并求出最省钱的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠BAC=90°AB=AC,分别过点B、C做经过点A的直线的垂线BD、CE,若BD=14cm,CE=3cm,则DE=_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=ax+b(a≠0)、二次函数y=ax2+bx和反比例函数y=![]() (k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(-2,0),则下列结论中,正确的是( )
(k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(-2,0),则下列结论中,正确的是( )

A.b=2a+k B.a=b+k C.a>b>0 D.a>k>0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com