
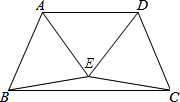
 如图,△ABE与△CDE是两个全等的等边三角形,且EA⊥ED.有下列四个结论:(1)∠EBC=15°;(2)AD∥BC;(3)直线CE与AB垂直;(4)四边形ABCD是轴对称图形.其中正确的结论有( )
如图,△ABE与△CDE是两个全等的等边三角形,且EA⊥ED.有下列四个结论:(1)∠EBC=15°;(2)AD∥BC;(3)直线CE与AB垂直;(4)四边形ABCD是轴对称图形.其中正确的结论有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 (1)先求出∠BPC的度数是360°-60°×2-90°=150°,再根据对称性得到△BPC为等腰三角形,∠PBC即可求出;根据题意:有△APD是等腰直角三角形;△PBC是等腰三角形;结合轴对称图形的定义与判定,可得四边形ABCD是轴对称图形,进而可得②③④正确
解答 解:∵△ABP≌△CDP,
∴AB=CD,AP=DP,BP=CP.
∵△ABP与△CDP是两个等边三角形,
∴∠PAB=∠PBA=∠APB=60°.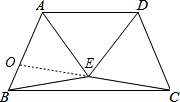
(1)根据题意,∠BPC=360°-60°×2-90°=150°
∵BP=PC,
∴∠PBC=(180°-150°)÷2=15°,
故本选项正确;
(2)∵∠ABC=60°+15°=75°,
∵AP=DP,
∴∠DAP=45°,
∵∠BAP=60°,
∴∠BAD=∠BAP+∠DAP=60°+45°=105°,
∴∠BAD+∠ABC=105°+75°=180°,
∴AD∥BC;
故本选项正确;
(3)延长CP交于AB于点O.
∠APO=180°-(∠APD+∠CPD)=180°-(90°+60°)=180°-150°=30°,
∵∠PAB=60°,
∴∠AOP=30°+60°=90°,
故本选项正确;
(4)根据题意可得四边形ABCD是轴对称图形,
故本选项正确.
综上所述,以上四个命题都正确.
故选A.
点评 本题考查了全等三角形的性质的运用,等边三角形的性质的运用,平行线的判定的运用,轴对称图形的定义与判定,如果一个图形沿着一条直线对折,两侧的图形能完全重合,这个图形就是轴对称图形.折痕所在的这条直线叫做对称轴.


科目:初中数学 来源: 题型:选择题
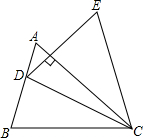 如图,把△ABC绕着点C顺时针旋转20°,得到△EDC,DE交AC于点H,若AC⊥DE,则∠A的度数是( )
如图,把△ABC绕着点C顺时针旋转20°,得到△EDC,DE交AC于点H,若AC⊥DE,则∠A的度数是( )| A. | 50° | B. | 60° | C. | 70° | D. | 75° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在小山的东侧A点处有一个热气球,由于受西风的影响,以30米/分的速度沿与地面成75°角的方向飞行,25分钟后到达C点处,此时热气球上的人测得小山西侧B点的俯角为30°,求小山东西两侧A、B两点间的距离.
如图,在小山的东侧A点处有一个热气球,由于受西风的影响,以30米/分的速度沿与地面成75°角的方向飞行,25分钟后到达C点处,此时热气球上的人测得小山西侧B点的俯角为30°,求小山东西两侧A、B两点间的距离.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,A、B两点的纵坐标分别为7和1,直线AB与y轴所夹锐角为60°,反比例函数y=$\frac{k}{x}$(x>0)的图象经过A、B两点,则k的值是7$\sqrt{3}$.
如图,在平面直角坐标系中,A、B两点的纵坐标分别为7和1,直线AB与y轴所夹锐角为60°,反比例函数y=$\frac{k}{x}$(x>0)的图象经过A、B两点,则k的值是7$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
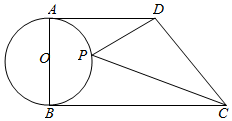 已知:AB是⊙O的直径,AD、BC是⊙O的切线,P是⊙O上一动点,若AD=5,AB=4,BC=8,则△PCD的面积的最小值是( )
已知:AB是⊙O的直径,AD、BC是⊙O的切线,P是⊙O上一动点,若AD=5,AB=4,BC=8,则△PCD的面积的最小值是( )| A. | 2 | B. | 4 | C. | 8 | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com