
| A. | ±1 | B. | ±9 | C. | 1或9 | D. | -1或-9 |
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
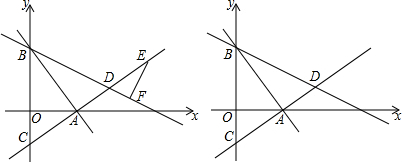
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
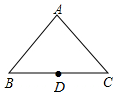 如图,在△ABC中,AB=AC=5,D是BC的中点,现在以D为圆心,以DC为半径作⊙D,求:
如图,在△ABC中,AB=AC=5,D是BC的中点,现在以D为圆心,以DC为半径作⊙D,求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
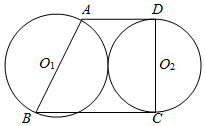 如图,已知梯形ABCD中,AD∥BC,DC⊥BC,AB=10,tanB=$\frac{4}{3}$,⊙O1以AB为直径,⊙O2以CD为直径,且⊙O1与⊙O2相切,求AD的长.
如图,已知梯形ABCD中,AD∥BC,DC⊥BC,AB=10,tanB=$\frac{4}{3}$,⊙O1以AB为直径,⊙O2以CD为直径,且⊙O1与⊙O2相切,求AD的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
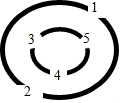 如图,某学校九年级数学兴趣小组组织一次数学活动.在一座有三道环形路的数字迷宫的每个进口处都标记着一个数,要求进入者把自己当做数“1”,进入时必须乘进口处的数,并将结果带到下一个进口,依次累乘下去,在通过最后一个进口时,只有乘积是5的倍数,才可以进入迷宫中心,现让小军从最外环任一个进口进入.
如图,某学校九年级数学兴趣小组组织一次数学活动.在一座有三道环形路的数字迷宫的每个进口处都标记着一个数,要求进入者把自己当做数“1”,进入时必须乘进口处的数,并将结果带到下一个进口,依次累乘下去,在通过最后一个进口时,只有乘积是5的倍数,才可以进入迷宫中心,现让小军从最外环任一个进口进入.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com