

���� ��1���ȸ����������������y=$\frac{1}{4}$x2�Ľ���ΪF��0��1������ֱ��y=kx+1����F��0��1�������߶�A��B���е�ΪM������AMB�ֱ�����l�Ĵ��ߣ�����ֱ�ΪG��N��H����AG��MN��BH����������λ�߶�����֪��MN=$\frac{1}{2}$��AG+BH�����ɲ���֪��AF=AG��BF=BH������ֱ��AB=AF+BF=AG+BH��֪MN=$\frac{1}{2}$AB=R����Բ�ĵ��ߵľ�����ڰ뾶���ɴ˿ɵó����ۣ�
��2�����ݵ�k=0��֪AB��x��ƽ�У���F��0��1�����ɵó�AB=4���ɣ�1��֪����ABΪֱ����Բ�������У��е�ΪK������DK�����EKD=��FKC=90�㣬��FE=FK=FD����FKC=��CEK�����ݹ��ɶ��������EC��EM��MC�ij������������ε������ʽ���ɵó����ۣ�
���  ��1��֤����������֪��������y=$\frac{1}{4}$x2�Ľ���ΪF��0��1����
��1��֤����������֪��������y=$\frac{1}{4}$x2�Ľ���ΪF��0��1����
��ֱ��y=kx+1����F��0��1����
���߶�A��B���е�ΪM������AMB�ֱ�����l�Ĵ��ߣ�����ֱ�ΪG��N��H����AG��MN��BH��
��MN=$\frac{1}{2}$��AG+BH����
�ɲ���֪��AF=AG��BF=BH��
��ֱ��AB=AF+BF=AG+BH��
��MN=$\frac{1}{2}$AB=R����Բ�ĵ��ߵľ�����ڰ뾶��
����ABΪֱ����Բ����l���У�
��2���⣺��ͼ2��
�ߵ�k=0ʱ��AB��x��ƽ�У�
��F��0��1����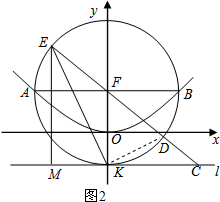
��AB=4��
���ɣ�1��֪����ABΪֱ����Բ�������У��е�ΪK��
����DK�����EKD=��FKC=90�㣬
��FE=FK=FD��
���FKC=��CEK��
�ߡ�MCE=��CEK����FCK=30�㣬
��FC=4��
��EC=6��EM=3��MC=3$\sqrt{3}$��
��S��MCE=$\frac{1}{2}$MC•ME=$\frac{1}{2}$��3$\sqrt{3}$��3=$\frac{9\sqrt{3}}{2}$��
���� ���⿼����Ƕ��κ����ۺ��⣬�����������������ߣ���������μ�ֱ�������Σ��ٸ���������λ�߶�����֪ʶ����ǽ�����Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��4����ͬ��С�������ɵļ�������ͼ��ʾ������������ͼ�ǣ�������
��4����ͬ��С�������ɵļ�������ͼ��ʾ������������ͼ�ǣ�������| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ڡ�ABC�У���ABC=45�㣬AD�ǡ�BAC��ƽ���ߣ�EF��ֱƽ��AD��BC���ӳ�����F�����CAF�Ķ����ǣ�������
��ͼ���ڡ�ABC�У���ABC=45�㣬AD�ǡ�BAC��ƽ���ߣ�EF��ֱƽ��AD��BC���ӳ�����F�����CAF�Ķ����ǣ�������| A�� | 30�� | B�� | 45�� | C�� | 75�� | D�� | 60�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��CE��BD��DE��AC����AC=8�����ı���CODE���ܳ���������
��ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��CE��BD��DE��AC����AC=8�����ı���CODE���ܳ���������| A�� | 8 | B�� | 12 | C�� | 16 | D�� | 20 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 45�� | B�� | 60�� | C�� | 90�� | D�� | 180�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com