
 如图,点A(2,m)在双曲线y=$\frac{k}{x}$上,AB⊥x轴,B为垂足,tan∠AOB=2.
如图,点A(2,m)在双曲线y=$\frac{k}{x}$上,AB⊥x轴,B为垂足,tan∠AOB=2.分析 (1)根据点A(2,m),AB⊥x轴,tan∠AOB=2可得出OB及AB的长,故可得出A点坐标,代入反比例函数的解析式即可;
(2)设C(x,0),则P(x,$\frac{8}{x}$),再分△AOB∽△PBC与△AOB∽△BPC两种情况进行讨论.
解答  解:(1)∵点A(2,m),AB⊥x轴,tan∠AOB=2,
解:(1)∵点A(2,m),AB⊥x轴,tan∠AOB=2,
∴OB=2,AB=4,
∴A(2,4).
∵点A(2,4)在双曲线y=$\frac{k}{x}$上,
∴k=2×4=8,
∴双曲线的解析式为y=$\frac{8}{x}$;
(2)设C(x,0),则P(x,$\frac{8}{x}$),
则一定有△AOB∽△PBC,
则$\frac{AB}{PC}$=$\frac{OB}{BC}$,即$\frac{4}{\frac{8}{x}}$=$\frac{2}{x-2}$,解得:x=1+$\sqrt{5}$或1-$\sqrt{5}$(舍去)
则P的坐标是(1+$\sqrt{5}$,2$\sqrt{5}$-2);
当△AOB∽△BPC时,$\frac{AB}{BC}$=$\frac{OB}{PC}$,则$\frac{4}{x-2}$=$\frac{2}{\frac{8}{x}}$,解得:x=4或-2(舍去),
则P的坐标是(4,2).
综上所述,符合条件的P点坐标为:P1(1+$\sqrt{5}$,2$\sqrt{5}$-2),P2(4,2).
点评 本题考查的是反比例函数综合题,在解答此题时要注意进行分类讨论,不要漏解.


科目:初中数学 来源: 题型:解答题
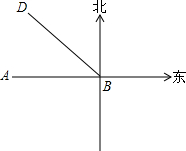 由于过度砍伐森林和破坏植被,我国某些地区经常受到沙尘暴的侵袭,如图,某日A市气象局测得沙尘暴中心在A市正东方向400km的B处,正向西北方向移动,移动速度为20km/h,距沙尘暴中心300km的范围内将受到影响,问A市是否会受到这次沙尘暴的影响?影响时间多长?
由于过度砍伐森林和破坏植被,我国某些地区经常受到沙尘暴的侵袭,如图,某日A市气象局测得沙尘暴中心在A市正东方向400km的B处,正向西北方向移动,移动速度为20km/h,距沙尘暴中心300km的范围内将受到影响,问A市是否会受到这次沙尘暴的影响?影响时间多长?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com