
【题目】定义:有且仅有一组对角相等的凸四边形叫做“准平行四边形”.例如:凸四边形![]() 中,若
中,若![]() ,则称四边形
,则称四边形![]() 为准平行四边形.
为准平行四边形.
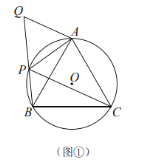
(1)如图①,![]() 是
是![]() 上的四个点,
上的四个点,![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() .求证:四边形
.求证:四边形![]() 是准平行四边形;
是准平行四边形;
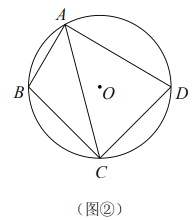
(2)如图②,准平行四边形![]() 内接于
内接于![]() ,
,![]() ,若
,若![]() 的半径为
的半径为![]() ,求
,求![]() 的长;
的长;
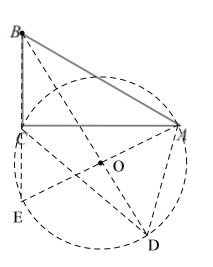
(3)如图③,在![]() 中,
中,![]() ,若四边形
,若四边形![]() 是准平行四边形,且
是准平行四边形,且![]() ,请直接写出
,请直接写出![]() 长的最大值.
长的最大值.

【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)先根据同弧所对的圆周角相等证明三角形ABC为等边三角形,得到∠ACB=60°,再求出∠APB=60°,根据AQ=AP判定△APQ为等边三角形,∠AQP=∠QAP=60°,故∠ACB=∠AQP,可判断∠QAC>120°,∠QBC<120°,故∠QAC≠∠QBC,可证四边形![]() 是准平行四边形;
是准平行四边形;
(2)根据已知条件可判断∠ABC≠∠ADC,则可得∠BAD=∠BCD=90°,连接BD,则BD为直径为10,根据BC=CD得△BCD为等腰直角三角形,则∠BAC=∠BDC=45°,在直角三角形BCD中利用勾股定理或三角函数求出BC的长,过B点作BE⊥AC,分别在直角三角形ABE和△BEC中,利用三角函数和勾股定理求出AE、CE的长,即可求出AC的长.
(3)根据已知条件可得:∠ADC=∠ABC=60°,延长BC 到E点,使BE=BA,可得三角形ABE为等边三角形,∠E=60°,过A、E、C三点作圆o,则AE为直径,点D在点C另一侧的弧AE上(点A、点E除外),连接BO交弧AE于D点,则此时BD的长度最大,根据已知条件求出BO、OD的长度,即可求解.
(1)∵![]()
∴∠ABC=∠BAC=60°
∴△ABC为等边三角形,∠ACB=60°
∵∠APQ=180°-∠APC-∠CPB=60°
又AP=AQ
∴△APQ为等边三角形
∴∠AQP=∠QAP=60°
∴∠ACB=∠AQP
∵∠QAC=∠QAP+∠PAB+∠BAC=120°+∠PAB>120°
故∠QBC=360°-∠AQP-∠ACB-∠QAC<120°
∴∠QAC≠∠QBC
∴四边形![]() 是准平行四边形
是准平行四边形
(2)连接BD,过B点作BE⊥AC于E点
∵准平行四边形![]() 内接于
内接于![]() ,
,![]()
∴∠ABC≠∠ADC,∠BAD=∠BCD
∵∠BAD+∠BCD=180°
∴∠BAD=∠BCD=90°
∴BD为![]() 的直径
的直径
∵![]() 的半径为5
的半径为5
∴BD=10
∵BC=CD,∠BCD=90°
∴∠CBD=∠BDC=45°
∴BC=BD![]() sin∠BDC=10
sin∠BDC=10![]() ,∠BAC=∠BDC=45°
,∠BAC=∠BDC=45°
∵BE⊥AC
∴∠BEA=∠BEC=90°
∴AE=AB![]() sin∠BAC=6
sin∠BAC=6![]()
![]()
∵∠ABE=∠BAE=45°
∴BE=AE=![]()
在直角三角形BEC中,EC=![]()
∴AC=AE+EC=![]()
(3)在![]() 中,
中,![]()
∴∠ABC=60°
∵四边形![]() 是准平行四边形,且
是准平行四边形,且![]()
∴∠ADC=∠ABC=60°
延长BC 到E点,使BE=BA,可得三角形ABE为等边三角形,∠E=60°,过A、E、C三点作圆o,因为∠ACE=90°,则AE为直径,点D在点C另一侧的弧AE上(点A、点E除外),此时,∠ADC=∠AEC=60°,连接BO交弧AE于D点,则此时BD的长度最大.
在等边三角形ABE中,∠ACB=90°,BC=2
∴AE=BE=2BC=4
∴OE=OA=OD=2
∴BO⊥AE
∴BO=BE![]() sin∠E=4
sin∠E=4![]()
∴BD=BO+0D=2+![]()
即BD长的最大值为2+![]()


科目:初中数学 来源: 题型:
【题目】如图(1),在△ABC中,如果正方形PQMN的边QM在BC上,顶点P,N分别在AB,AC上,那么我们称这样的正方形为“三角形内接正方形”小波同学按数学家波利亚在《怎样解题》中的方法进行操作:如图(2),任意画△ABC,在AB上任取一点P′,画正方形P′Q′M′N′,使Q′,M′在BC边上,N′在△ABC内,连结BN′并延长交AC于点N,画NM⊥BC于点M,NP⊥NM交AB于点P,PQ⊥BC于点Q,得到四边形PQMN,小波把线段BN称为“波利亚线”,请帮助小波解决下列问题:
(1)四边形PQMN是否是△ABC的内接正方形,请证明你的结论;
(2)若△ABC为等边三角形,边长BC=6,求△ABC内接正方形的边长;
(3)如图(3),若在“波利亚线”BN上截取NE=NM,连结EQ,EM.当![]() 时,猜想∠QEM的度数,并说明你的理由.
时,猜想∠QEM的度数,并说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的纸箱里有分别标有汉字“热”“爱”“祖”“国”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先摇匀再摸球.
(1)若从中任取一个球,求摸出球上的汉字刚好是“国”字的概率;
(2)小红从中任取球,不放回,再从中任取一球,请用树状图或列表法,求小红取出的两个球上的汉字恰好能组成“爱国”或“祖国”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校七年级学生作业时间情况,随机抽取了该校七年级部分学生进行调查,并根据调查结果绘制了如下的统计图.
作业时间分组表(单位:小时)
别 | 作业时间 | 人数 | 频率 |
A | 1≤x≤1.5 | 5 | 0.1 |
B | 1.5≤x≤2 | 20 | b |
C | 2≤x≤2.5 | m | n |
D | x≥2.5 | 7 | 0.14 |
小计 | a | 1 |
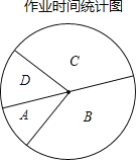
(1)统计图中的a=______;b=______;m=______;n=______.
(2)求出C组的扇形的圆心角度数.
(3)如果该校七年级学生共400名,试估计这400名生作业时间在B组和C组的人数共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
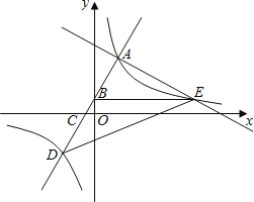
【题目】如图,直线y=2x+b与双曲线y=![]() (k>0)交于点A、D,直线AD交y轴、x轴于点B、C,直线y=-
(k>0)交于点A、D,直线AD交y轴、x轴于点B、C,直线y=-![]() +n过点A,与双曲线y=
+n过点A,与双曲线y=![]() (k>0)的另一个交点为点E,连接BE、DE,若S△ABE=4,且S△ABE:S△DBE=3:4,则k的值为___.
(k>0)的另一个交点为点E,连接BE、DE,若S△ABE=4,且S△ABE:S△DBE=3:4,则k的值为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天晚上,小颖由路灯A下的B处向正东走到C处时,测得影子CD的长为1米.当她继续向正东走到D处时,测得此时影子DE的一端E到路灯A的仰角为45°.已知小颖的身高为1.5米,那么路灯AB的高度是多少米?( )
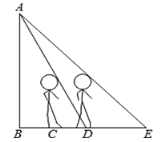
A.4米B.4.5米C.5米D.6米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】怡然美食店的A、B两种菜品,每份成本均为14元,售价分别为20元、18元,这两种菜品每天的营业额共为1120元,总利润为280元.
(1)该店每天卖出这两种菜品共多少份?
(2)该店为了增加利润,准备降低A种菜品的售价,同时提高B种菜品的售价,售卖时发现,A种菜品售价每降0.5元可多卖1份;B种菜品售价每提高0.5元就少卖1份,如果这两种菜品每天销售总份数不变,那么这两种菜品一天的总利润最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
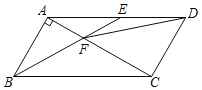
【题目】如图,在ABCD中,∠BAC=90°,∠ABC=60°,E是AD的中点,连结BE交对角线AC于点F,连结DF,则tan∠DFE的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com