
����Ŀ���Ķ����в��Ͻ�����⣺������λ�������������Ǹ���λ�ϵ�����֮����ȣ������������λ����Ϊ����������������37��82�����Ǹ���λ�ϵ�����֮�ͷֱ�Ϊ3+7��8+2����Ȼ3+7��8+2��10��37��82��Ϊ������������
��1������˵����������� ��
A.123��51���������� �� B.345��513������������ C.2018��8120�������������� D�����![]() ��
��![]() ������������
������������
��2����A��B���������ȵ���λ����A��![]() ��B��
��B��![]() ��A��B��Ϊ��������������A��B֮����B��A֮���3������֤��y=-x+9.
��A��B��Ϊ��������������A��B֮����B��A֮���3������֤��y=-x+9.
���𰸡���1��B����2��������.
��������
��1���������⣬������λ�������������Ǹ���λ�ϵ�����֮����ȣ������������λ����Ϊ��������������������
��2�����á������������ó�x+y=m+n��������A��B֮����B��A֮���3�����ó�x+y=9(m-2x)����x+y��9�ı������ó����۳���.
�⣺��1�����ݵ������Ķ��壬ͨ�������λ��֮�ͣ���֪Bѡ�����
��ѡ��B��
��2��֤�����������֪��![]() ��
��
����x+y=9(m-2x)����x+y��9�ı�����
����x+y=9��18��
����y=-x+9.


 �Ƹ������������ϵ�д�
�Ƹ������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���±���ij��ѧ���꼶5��ѧ�������������
���� | Сӱ | С�� | С�� | С�� | С�� |
���أ�ǧ�ˣ� | 34 | 45 | |||
������ƽ�����صIJ� | -6 | +3 | -4 | 0 |
��1������ϱ�.
��2��˭���أ�˭���
��3�����ص�������������٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڽ��ꡰ��ɫ�������������롱��У�ij������![]() Ԫ�������ɾջ����ܿ����꣬��������
Ԫ�������ɾջ����ܿ����꣬��������![]() Ԫ�����ڶ����ջ�����֪�ڶ����������ջ��������ǵ�һ���������ջ�������
Ԫ�����ڶ����ջ�����֪�ڶ����������ջ��������ǵ�һ���������ջ�������![]() ������ÿ��ջ��Ľ��۱ȵ�һ��ÿ��ջ��Ľ��۶�
������ÿ��ջ��Ľ��۱ȵ�һ��ÿ��ջ��Ľ��۶�![]() Ԫ.
Ԫ.
��1�����һ��ÿ��ƿ�ջ��Ľ����Ƕ���Ԫ��
��2������һ��ÿ��ջ���![]() Ԫ�ۼ����ۣ�Ҫʹ��������
Ԫ�ۼ����ۣ�Ҫʹ��������![]() Ԫ���������������أ����ڶ���ÿ��ջ����ۼ������Ƕ���Ԫ��
Ԫ���������������أ����ڶ���ÿ��ջ����ۼ������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Բ���β���������Ϊ![]() �������ܳ�Ϊ
�������ܳ�Ϊ![]() ���ڱ����뱭��
���ڱ����뱭��![]() �ĵ�
�ĵ�![]() ����һ�η��ۣ���ʱһֻ���������ڱ���ڣ��뱭����
����һ�η��ۣ���ʱһֻ���������ڱ���ڣ��뱭����![]() �������Եĵ�
�������Եĵ�![]() ���������ϵ�����۵���̾���Ϊ( )
���������ϵ�����۵���̾���Ϊ( )![]() .
.
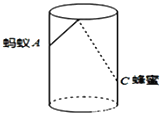
A. 15B. ![]() C. 12D. 18
C. 12D. 18
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACB=90����CD��AB����ΪD��AEƽ�֡�CAB��CD�ڵ�F����BC�ڵ�E��EH��AB������ΪH������FH��
(1)��֤��CF=CE
(2)���ж��ı���CFHE����״����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y��2x+6��x����A����y����B��

��1��ֱ��д��A���� ������ ������B���� ������ ������
��2����ͼ1����EΪֱ��y��x+2��һ�㣬��FΪֱ��y��![]() x��һ�㣬����A��B��E��FΪ������ı�����ƽ���ı��Σ����E��F������
x��һ�㣬����A��B��E��FΪ������ı�����ƽ���ı��Σ����E��F������
��3����ͼ2����C��m��n��Ϊ�߶�AB��һ���㣬D����7m��0����x���ϣ�����CD����MΪCD���е㣬���M��������y�ͺ�����x֮��ĺ�����ϵʽ����ֱ��д���ڵ�C�ƶ������е�M���˶�·������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��װ������һ�ּп˺�T�����п�ÿ������120Ԫ��T��ÿ������60Ԫ�������ڿ�չ������ڼ䣬��ͻ��ṩ�����Żݷ���������һ���п���һ��T�����ڼп˺�T���������۵�80%�����ij�ͻ�Ҫ���÷�װ������п�30����T��![]() ����
����![]() ��30����
��30����
��1�����ÿͻ��������ٹ����踶���� �� Ԫ���ú�x�Ĵ���ʽ��ʾ����
���ÿͻ��������ڹ����踶���� �� Ԫ���ú�x�Ĵ���ʽ��ʾ����
��2����![]() =40��ͨ������˵���������١����������ַ��������Ϊ���㣿
=40��ͨ������˵���������١����������ַ��������Ϊ���㣿
��3���������Żݷ�����ͬʱʹ�ã���![]() =40ʱ�����ܸ���һ�ָ�ΪʡǮ�Ĺ�������д����Ĺ�������˵�����ɣ�
=40ʱ�����ܸ���һ�ָ�ΪʡǮ�Ĺ�������д����Ĺ�������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������������ͬ���ļ۸����ͬ������Ʒ���������Ƴ���ͬ���Żݷ������ڼ׳����ۼƹ��ﳬ��100Ԫ����100Ԫ�IJ��ְ�80%�շѣ����ҳ����ۼƹ��ﳬ��50Ԫ����50Ԫ�IJ��ְ�90%�շ�.��С����ͬһ�����ۼƹ���![]() Ԫ�����ڼ׳��й���ʵ�ʸ���
Ԫ�����ڼ׳��й���ʵ�ʸ���![]() (Ԫ).���ҳ��й���ʵ�ʸ���
(Ԫ).���ҳ��й���ʵ�ʸ���![]() (Ԫ).
(Ԫ).
(1)�ֱ����![]() ��
��![]() ��
��![]() �ĺ�����ϵʽ.
�ĺ�����ϵʽ.
(2)����С���ۼƹ�����ı仯�����������ļҳ��й��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
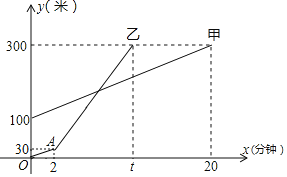
����Ŀ���ס���������Լ��ĩ��ͬһ��·�ߵ�ɽ���ס������˾����ĸ߶�y���ף����ɽʱ��x�����ӣ�֮��ĺ���ͼ����ͼ��ʾ������ͼ�����ṩ����Ϣ�����������
��1����ɽ���ٶ���ÿ������ �ף�����A������ʱ�������ĸ߶�Ϊ�� �ף�
��2���������ٺ��ҵ��ٶ��Ǽ�ɽ�ٶȵ�3����
�����ҵ�ɽȫ�����У���ɽʱ�����ĸ߶�y���ף����ɽʱ��x�����ӣ�֮��ĺ�������ʽ��
���Ҽƻ��������ٺ�5�������ϼף����ж��ҵļƻ���ʵ���𣿲�˵�����ɣ�
��3����xΪ����ʱ���ס������˾����ĸ߶Ȳ�Ϊ80�ף�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com