
 如图,在Rt△ABC中∠ABC=90°,以AB为直径作圆O交AC于E,连接E点和CB的中点D.
如图,在Rt△ABC中∠ABC=90°,以AB为直径作圆O交AC于E,连接E点和CB的中点D.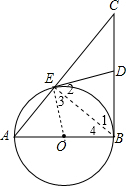
| AE |
| AB |
| AB |
| AC |
| 4 |
| 6 |
| 6 |
| AC |
| AC2-AB2 |
| 5 |


 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
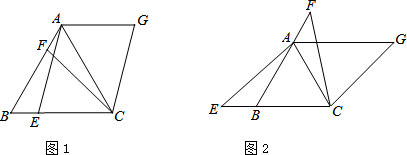
 如图,△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、F,连接BD交0F于点E.
如图,△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、F,连接BD交0F于点E.| 5 |
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知,在Rt△ABC中,∠ABC=90°,D是AC的中点,⊙O经过A,D,B三点,CB的延长线交⊙O于点E,延长AC至F,使得CF=CD,连接EF
已知,在Rt△ABC中,∠ABC=90°,D是AC的中点,⊙O经过A,D,B三点,CB的延长线交⊙O于点E,延长AC至F,使得CF=CD,连接EF| CE |
| CD |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
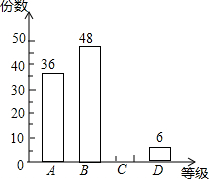 某校为了选拔省教委组织的以“爱我省会•让节能环保称为时尚”为主题的参赛作品,现在本校组织了一次“以爱我家乡•让节能环保成为时尚”的作品征集活动,现从所收集上来的作品中随机爱抽取了一部分,按A,B,C,D四个等级进行评选,并根据评选结果绘制了如图所示的条形统计图,已知等级C的作品的所抽取作品中占25%.
某校为了选拔省教委组织的以“爱我省会•让节能环保称为时尚”为主题的参赛作品,现在本校组织了一次“以爱我家乡•让节能环保成为时尚”的作品征集活动,现从所收集上来的作品中随机爱抽取了一部分,按A,B,C,D四个等级进行评选,并根据评选结果绘制了如图所示的条形统计图,已知等级C的作品的所抽取作品中占25%.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com