
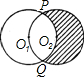
 (2004•包头)如图,两个等圆的圆心分别为O1、O2,⊙O1过点O2,两圆相交于P、Q两点,已知01O2=6cm,则阴影部分的周长是
(2004•包头)如图,两个等圆的圆心分别为O1、O2,⊙O1过点O2,两圆相交于P、Q两点,已知01O2=6cm,则阴影部分的周长是 |
| PQ |
 |
| PQ |
 |
| PQ |
 |
| PQ |

 |
| PQ |
| 120•π•6 |
| 180 |


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
 (2004•包头)如图,为了确定一条河的宽度AB,可以在点B一侧的岸边选择一点C,使得CB⊥AB,并量得CB=40米,测得∠ACB=45°,那么河的宽度AB是( )
(2004•包头)如图,为了确定一条河的宽度AB,可以在点B一侧的岸边选择一点C,使得CB⊥AB,并量得CB=40米,测得∠ACB=45°,那么河的宽度AB是( )查看答案和解析>>
科目:初中数学 来源: 题型:
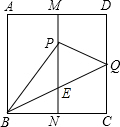 (2004•包头)如图,正方形ABCD的边长为6cm,M、N分别为AD、BC边的中点,将点C折至MN上,落在点P处,折痕BQ交MN于点E,则BE的长等于
(2004•包头)如图,正方形ABCD的边长为6cm,M、N分别为AD、BC边的中点,将点C折至MN上,落在点P处,折痕BQ交MN于点E,则BE的长等于| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2009年黑龙江省牡丹江市中考数学二模试卷(解析版) 题型:选择题
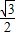

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com