
【题目】某中学开展“阳光体育一小时”活动,根据学校实际情况,决定开设A:踢毽子;B:篮球:C:跳绳;D:乒乓球四种运动项目.为了解学生最喜欢哪一种运动项目,随机抽取了一部分学生进行调查,并将调查结果绘制成如两个统计图.请结合图中的信息解答下列问题:
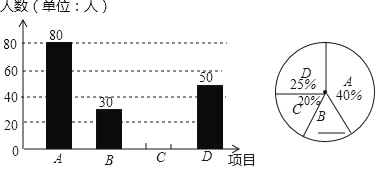
(1)本次共调查了多少名学生?
(2)请将两个统计图补充完整.
(3)求图中“A”层次所在扇形的圆心角的度数.
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
【题目】将正方体骰子(相对面上的点数分别为1和6、2和5、3和4)放置于水平桌面上,如图1。在图2中,将骰子向右翻滚90°,然后在桌面上按逆时针方向旋转90°,则完成一次变换。若骰子的初始位置为图1所示的状态,那么按上述规则连续完成14次变换后,骰子朝上一面的点数是_____________________。

查看答案和解析>>
科目:初中数学 来源: 题型:
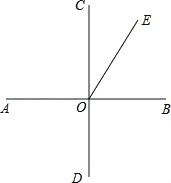
【题目】如图,AB垂直CD(即∠AOC=∠AOD=∠BOD=∠BOC=90°)
(1)比较∠AOD,∠EOB,∠AOE大小(用“<”连接)
(2)如∠EOC=28°,求∠EOB和∠EOD的度数(适当写出解题过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)如图①,四边形ABCD是正方形,点G是BC上的任意一点,BF⊥AG于点F,DE⊥AG于点E,探究BF,DE,EF之间的数量关系,第一学习小组合作探究后,得到DE﹣BF=EF,请证明这个结论; 
(2)若(1)中的点G在CB的延长线上,其余条件不变,请在图②中画出图形,并直接写出此时BF,DE,EF之间的数量关系; 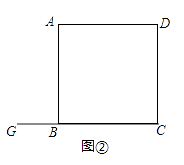
(3)如图③,四边形ABCD内接于⊙O,AB=AD,E,F是AC上的两点,且满足∠AED=∠BFA=∠BCD,试判断AC,DE,BF之间的数量关系,并说明理由 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线PQ∥MN,点A在PQ上,直角△BEF的直角边BE在MN上,且∠B=90°,∠BEF=30°.现将△BEF绕点B以每秒1°的速度按逆时针方向旋转(E,F的对应点分别是E′,F′),同时,射线AQ绕点A以每秒4°的速度按顺时针方向旋转(Q的对应点是Q′).设旋转时间为t秒(0≤t≤45).
(1)∠MBF′=__.(用含t的代数式表示)
(2)在旋转的过程中,若射线AQ′与边E′F′平行时,则t的值为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线![]() 分别与y轴、x轴交于点A、点B,点C的坐标为(-3,0),D为直线AB上一动点,连接CD交y轴于点E.
分别与y轴、x轴交于点A、点B,点C的坐标为(-3,0),D为直线AB上一动点,连接CD交y轴于点E.
(1) 点B的坐标为__________,不等式![]() 的解集为___________
的解集为___________
(2) 若S△COE=S△ADE,求点D的坐标;
(3) 如图2,以CD为边作菱形CDFG,且∠CDF=60°.当点D运动时,点G在一条定直线上运动,请求出这条定直线的解析式.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com