
【题目】如图,AB是⊙O的直径,F是⊙O上一点,连接FO、FB.C为![]() 中点,过点C作CD⊥AB,垂足为D,CD交FB于点E,CG∥FB,交AB的延长线于点G.
中点,过点C作CD⊥AB,垂足为D,CD交FB于点E,CG∥FB,交AB的延长线于点G.
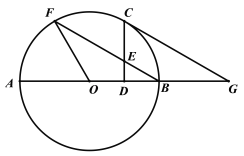
(1)求证:CG是⊙O的切线;
(2)若![]() BOF=120°,且CE=4,求⊙O的半径.
BOF=120°,且CE=4,求⊙O的半径.
【答案】(1)见解析;(2)⊙O的半径为4![]()
【解析】
(1)连接OC,利用垂径定理得到OC⊥BF,根据CG∥FB得到∠OCG=90°即可求解;
(2)连接BC,由(1)知,∠COB =60°,得到△OBC为等边三角形.,由CD⊥OB得到∠OCD=30°,求出EM=![]() CE=2,利用勾股定理求出CM=
CE=2,利用勾股定理求出CM=![]() ,再根据等腰三角形“三线合一”得OM=CM=
,再根据等腰三角形“三线合一”得OM=CM=![]() ,故OC=4
,故OC=4![]() ,即为半径长.
,即为半径长.
(1)证明:连接OC.
∵点C为![]() 的中点,
的中点,
∴![]() ,
,
所以∠COB=∠COF,
因为OB=OF,
所以OC⊥BF,
设垂足为M,则∠OMB=90°.
因为CG∥FB,
所以∠OCG=∠OMB=90°,
所以CG是⊙O的切线.
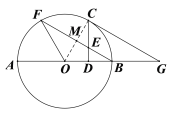
(2)解:连接BC.
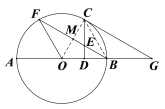
由(1)知,∠COB=∠COF=![]() ∠BOF=60°,
∠BOF=60°,
因为OB=OC,
所以△OBC为等边三角形,∠OCB=60°,
∵CD⊥OB,
∴CD平分∠OCB,
∴∠OCD=30°,
则EM=![]() CE=2,
CE=2,
又OC⊥BF,
所以CM=![]() .
.
∴OM=CM=![]() ,
,
所以OC=4![]() ,即⊙O的半径为4
,即⊙O的半径为4![]()


 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=8m,BC=6m,点P由C点出发以2m/s的速度向终点A匀速移动,同时点Q由点B出发以1m/s的速度向终点C匀速移动,当一个点到达终点时另一个点也随之停止移动.
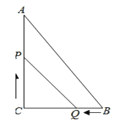
(1)经过几秒△PCQ的面积为△ACB的面积的![]() ?
?
(2)经过几秒,△PCQ与△ACB相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年女排世界杯中,中国女排以11站全胜且只丢3局的成绩成功卫冕本届世界杯冠军.某校七年级为了弘扬女排精神,组建了排球社团,通过测量同学们的身高(单位:cm),并绘制了如下两幅不完整的统计图,请结合图中提供的信息,解答下列问题.

(1)填空:样本容量为___,a=___;
(2)把频数分布直方图补充完整;
(3)若从该组随机抽取1名学生,估计这名学生身高低于165cm的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
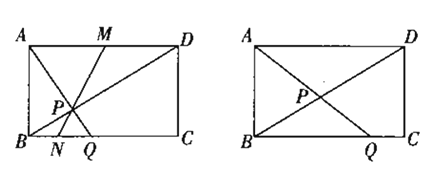
【题目】如图,矩形ABCD中,AB=a,AD=b,点P是对角线BD上的一个动点(点P不与B、D重合),连接AP并延长交射线BC于点Q,
(1)当AP⊥BD时,求△ABQ的面积(用含a、b的代数式表示).
(2)若点M为AD边的中点,连接MP交BC于点N,证明:点N也为线段BQ的中点.
(3)如图,当![]() 为何值时,△ADP与△BPQ的面积之和最小.
为何值时,△ADP与△BPQ的面积之和最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山,就是金山银山”,为了改善生态环境,某县政府准备对境内河流进行清淤、疏通河道,同时在人群密集区沿河流修建滨河步道,打造生态湿地公园.
(1)2018年11月至12月,一期工程原计划疏通河道和修建滨河步道里程数共计20千米,其中修建滨河步道里程数是疏通河道里程数的![]() 倍,那么,原计划修建滨河步道多少千米?
倍,那么,原计划修建滨河步道多少千米?
(2)至2018年12月底,一期工程顺利按原计划完成总共耗资840万元,其中疏通河道工程共耗资600万元;2019年二期工程开工后,疏通河道每千米工程费用较一期降低2.5a%,里程数较一期增加3a%;修建滨河步道每千米工程费用较一期上涨2.5a%,里程数较一期增加5a%,经测算,二期工程总费用将比一期增加2a%,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以坐标原点O为圆心,2为半径画![]() ,P是
,P是![]() 上一动点,且P在第一象限内,过点P作
上一动点,且P在第一象限内,过点P作![]() 的切线与x轴相交于点A,与y轴相交于点B.在
的切线与x轴相交于点A,与y轴相交于点B.在![]() 上存在点Q,使得以Q、O、A、P为顶点的四边形是平行四边形,请写出Q点的坐标_________.
上存在点Q,使得以Q、O、A、P为顶点的四边形是平行四边形,请写出Q点的坐标_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装超市购进单价为30元的童装若干件,物价部门规定其销售单价不低于每件30元,不高于每件60元.销售一段时间后发现:当销售单价为60元时,平均每月销售量为80件,而当销售单价每降低10元时,平均每月能多售出20件.同时,在销售过程中,每月还要支付其他费用450元.设销售单价为x元,平均月销售量为y件.
(1)求出y与x的函数关系式,并写出自变量x的取值范围.
(2)当销售单价为多少元时,销售这种童装每月可获利1800元?
(3)当销售单价为多少元时,销售这种童装每月获得利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①abc<0;②4ac<b2;③方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;④3a+c>0;⑤当y≥0时,x的取值范围是﹣1≤x≤3.其中结论正确的个数是( )
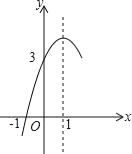
A. 1个B. 2个C. 3D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,AB=4.若△ABC固定不动,△AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合).
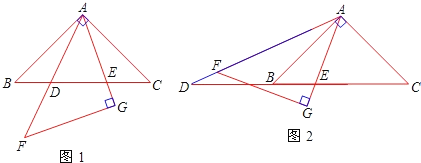
(1)求证:△ABE∽△DCA;
(2)若BE·CD=k(k为常数),求k的值;
(3)在旋转过程中,当△AFG旋转到如图2的位置时,AG与BC交于点E,AF的延长线与CB的延长线交于点D,那么(2)中k的值是否发生了变化?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com