
【题目】如图,若点M是![]() 轴正半轴上任意一点,过点M作PQ∥
轴正半轴上任意一点,过点M作PQ∥![]() 轴,分别交函数
轴,分别交函数![]() 和
和![]() 的图象于点P和Q,连接OP和OQ.则下列结论正确的是( )
的图象于点P和Q,连接OP和OQ.则下列结论正确的是( )

A.∠POQ不可能等于90°B.![]()
C.这两个函数的图象一定关于![]() 轴对称D.△POQ的面积是
轴对称D.△POQ的面积是![]()
科目:初中数学 来源: 题型:
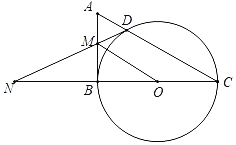
【题目】如图,在Rt△ABC中,以BC为直径的⊙O交AC于点D,过点D作⊙O的切线交AB于点M,交CB延长线于点N,连接OM,OC=1.
(1)求证:AM=MD;
(2)填空:
①若DN![]() ,则△ABC的面积为 ;
,则△ABC的面积为 ;
②当四边形COMD为平行四边形时,∠C的度数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
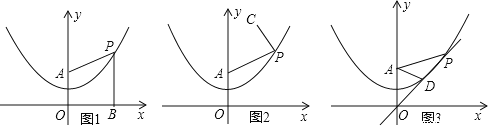
【题目】已知,在平面直角坐标系xOy中,点A的坐标为(0,2),点P(m,n)是抛物线![]() 上的一个动点.
上的一个动点.
(1)如图1,过动点P作PB⊥x轴,垂足为B,连接PA,请通过测量或计算,比较PA与PB的大小关系:PA_____PB(直接填写“>”“<”或“=”,不需解题过程);
(2)请利用(1)的结论解决下列问题:
①如图2,设C的坐标为(2,5),连接PC,AP+PC是否存在最小值?如果存在,求点P的坐标;如果不存在,简单说明理由;
②如图3,过动点P和原点O作直线交抛物线于另一点D,若AP=2AD,求直线OP的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图的![]() 中,
中,![]() ,且
,且![]() 为
为![]() 上一点.今打算在
上一点.今打算在![]() 上找一点
上找一点![]() ,在
,在![]() 上找一点
上找一点![]() ,使得
,使得![]() 与
与![]() 全等,以下是甲、乙两人的作法:
全等,以下是甲、乙两人的作法:
(甲)连接![]() ,作
,作![]() 的中垂线分别交
的中垂线分别交![]() 、
、![]() 于
于![]() 点、
点、![]() 点,则
点,则![]() 、
、![]() 两点即为所求
两点即为所求
(乙)过![]() 作与
作与![]() 平行的直线交
平行的直线交![]() 于
于![]() 点,过
点,过![]() 作与
作与![]() 平行的直线交
平行的直线交![]() 于
于![]() 点,则
点,则![]() 、
、![]() 两点即为所求
两点即为所求
对于甲、乙两人的作法,下列判断何者正确?( )

A. 两人皆正确B. 两人皆错误
C. 甲正确,乙错误D. 甲错误,乙正确
查看答案和解析>>
科目:初中数学 来源: 题型:
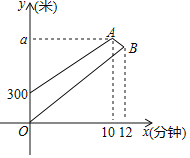
【题目】小明放学后从学校回家,出发![]() 分钟时,同桌小强发现小明的数学作业卷忘记拿了,立即拿着数学作业卷按照同样的路线去追赶小明,小强出发
分钟时,同桌小强发现小明的数学作业卷忘记拿了,立即拿着数学作业卷按照同样的路线去追赶小明,小强出发![]() 分钟时,小明才想起没拿数学作业卷,马上以原速原路返回,在途中与小强相遇.两人离学校的路程
分钟时,小明才想起没拿数学作业卷,马上以原速原路返回,在途中与小强相遇.两人离学校的路程![]() (米)与小强所用时间
(米)与小强所用时间![]() (分钟)之间的函数图象如图所示.
(分钟)之间的函数图象如图所示.
(1)求函数图象中![]() 的值;
的值;
(2)求小强的速度;
(3)求线段![]() 的函数解析式,并写出自变量的取值范围.
的函数解析式,并写出自变量的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(14分)如图1,△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,点B在线段AE上,点C在线段AD上.
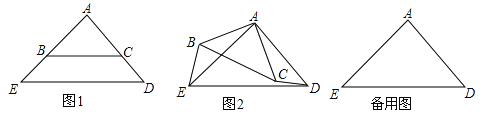
(1)请直接写出线段BE与线段CD的关系: ;
(2)如图2,将图1中的△ABC绕点A顺时针旋转角α(0<α<360°),
①(1)中的结论是否成立?若成立,请利用图2证明;若不成立,请说明理由;
②当AC=![]() ED时,探究在△ABC旋转的过程中,是否存在这样的角α,使以A、B、C、D四点为顶点的四边形是平行四边形?若存在,请直接写出角α的度数;若不存在,请说明理由.
ED时,探究在△ABC旋转的过程中,是否存在这样的角α,使以A、B、C、D四点为顶点的四边形是平行四边形?若存在,请直接写出角α的度数;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,将
上,将![]() 沿直线
沿直线![]() 折叠,点
折叠,点![]() 恰好落在
恰好落在![]() 边上的点
边上的点![]() 处,且
处,且![]() .
.
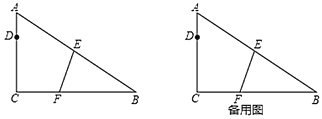
(1)求![]() 的长;
的长;
(2)点![]() 是射线
是射线![]() 上的一个动点,连接
上的一个动点,连接![]() ,
,![]() ,
,![]() ,
,![]() 的面积与
的面积与![]() 的面积相等,
的面积相等,
①当点![]() 在线段
在线段![]() 上时,求
上时,求![]() 的长;
的长;
②当点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() ________;
________;
(3)将直线![]() 平移,平移后的直线与直线
平移,平移后的直线与直线![]() ,直线
,直线![]() 分别交于点
分别交于点![]() 和点
和点![]() ,以线段
,以线段![]() 为一边作正方形
为一边作正方形![]() ,点
,点![]() 与点
与点![]() 在直线
在直线![]() 两侧,连接
两侧,连接![]() 当
当![]() 时,请直接写出
时,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD内部有若干个点,则用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
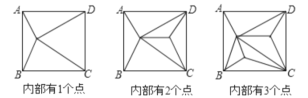
(1)填写下表:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | ... | n |
分割成三角形的个数 | 4 | 6 | _____ | _____ | ... | _____ |
(2)原正方形能否被分割成2021个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某路灯在铅垂面内的示意图,灯柱AB的高为13米,灯杆BC与灯柱AB的夹角∠B=120°,路灯采用锥形灯罩,在地面上的照射区域DE长为20米,已知tan∠CDE=![]() ,tan∠CED=
,tan∠CED=![]() ,求灯杆BC的长度.
,求灯杆BC的长度.
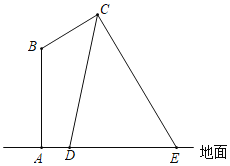
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com