
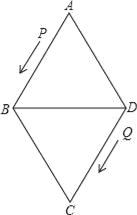
����Ŀ����ͼ������ABCD�ı߳�Ϊ24���ף���A=60������P�ӵ�A��������·AB��BD�������˶�����Q�ӵ�Dͬʱ��������·DC��CB��BA�������˶���
��1����BD�ij���
��2����֪��P��Q�˶����ٶȷֱ�Ϊ4����/�룬5����/�룬����12���P��Q�ֱ�M��N���㣬�����ǵĴ�С���з��࣬����ȷ����AMN����һ�������Σ���˵�����ɣ�
��3���裨2���еĵ�P��Q�ֱ��M��Nͬʱ��ԭ·���أ���P���ٶȲ��䣬��Q���ٶȸı�Ϊa����/�룬����3���P��Q�ֱ�E��F���㣬����BEF�루2���е���AMN���ƣ�����a��ֵ��
���𰸡���1��BD=24��2����AMN��ֱ�������Σ�3��2��6��12
�������������������1���������ε�����֤��ABD�ǵȱ������μ��ɣ�
��2�����P Q�ߵľ��룬�ٸ��ݵ������������ʼ����Ƴ��𰸣�
��3����Ϊ����������������ƣ��õ�����ʽ�����Q�ߵľ��룬��������𰸣�
�����������1��������ABCD��
��AB=AD��
�ߡ�A=60����
���ABD�ǵȱ������Σ�
��BD=AB=24���ף�
��BD=24���ף�
��2��12��ʱ��P����4��12=48��
��AB+BD=24+24=48��
��P��D�㣬
ͬ��Q��AB���е��ϣ�
��AD=BD��
��MN��AB��
���AMN��ֱ�������Σ�
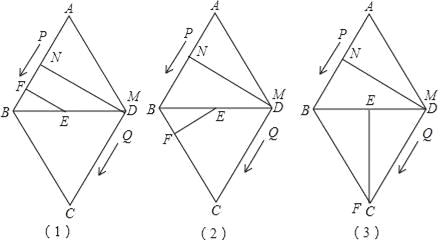
��3���������������ͼ��2��
��ANM=��EFB=90������A=��DBF=60����DE=3��4=12=![]() AD��
AD��
�����������������ʵã�BF=![]() AN=6��
AN=6��
��NB+BF=12+6=18��
��a=18��3=6��
ͬ������ͼ��1�����a=2��
��ͼ��3��a=12��
��a��ֵ��2��6��12��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABC�У�AB��AC��BD��AC���ϵ����ߣ����D���������ABC���ܳ���Ϊ12cm��15cm�����֣���������θ��ߵij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC��DE��EF���ۣ�����A��B�����ڵ�O������EA��EB�غ����߶�EO������CDO+��CFO=98�㣬���C�Ķ���Ϊ�� �� 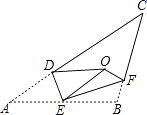
A.40��
B.41��
C.42��
D.43��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������߲˱������߲˵�����5��,�Ű�������2����߲˺�3�����߲�,һ������20Ԫ,���������߲˵ĵ���ΪxԪ/��,��ô���з�����ȷ����(����)
A. 2x+3(x+5)=20 B. 2x+3(x+0.5)=20 C. 2x+3(x-0.5)=20 D. 2x+3(x-5)=20
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ֱ��AB��CD��ֱ��l��ֱ��AB��CD�ཻ�ڵ�E��F����P������EA�ϵ�һ�����㣨�������˵�E��������EPF��PF�۵���ʹ����E���ڵ�Q���� 
��1������PEF=48�㣬��Fǡ���������е�һ��ƽ�����ϣ���ֱ��д����EFP�Ķ�����
��2������PEF=75�㣬��CFQ= ![]() ��PFC�����EFP�Ķ�����
��PFC�����EFP�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������4�֣������и����ֱ�������Ӧ�ļ����ڣ�
��2.5��0����0.5252252225����ÿ����5֮����������1��2����100%��������2����![]() ��
��![]()
��1���������ϣ��� ������
��2�����������ϣ��� ������
��3���������ϣ��� ������
��4�����������ϣ�{ ��}��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
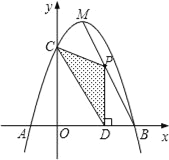
����Ŀ����ͼ��������y=��x2+bx+c��x���ཻ��A��B���㣬��y���ཻ�ڵ�C���ҵ�B���C������ֱ�ΪB��3��0����C��0��3������M�������ߵĶ��㣮
��1������κ����Ĺ�ϵʽ��
��2����PΪ�߶�MB��һ�����㣬����P��PD��x���ڵ�D����OD=m����PCD�����ΪS�����ж�S�����ֵ����Сֵ����˵�����ɣ�
��3����MB���Ƿ���ڵ�P��ʹ��PCDΪֱ�������Σ�������ڣ��������P�����ꣻ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����1=��2����GFA=55�㣬��ACB=75�㣬AQƽ�֡�FAC��AH��BD�����HAQ�Ķ����� 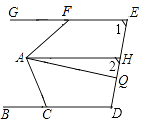
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com