
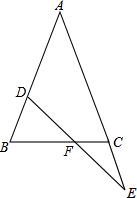
 如图,△ABC中,AB=AC,点D在AB上,点E在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CE.
如图,△ABC中,AB=AC,点D在AB上,点E在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CE.科目:初中数学 来源: 题型:
| 观察时间x | 该地区沙漠面积y(万公顷) |
| 第一年底 | 100.2 |
| 第二年底 | 100.4 |
| 第三年底 | 100.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
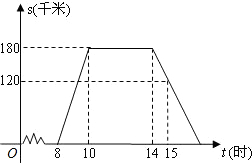 “国庆黄金周”的某一天,小明全家上午8时自驾小汽车从家里出发,到距离180千米的某著名旅游景点游玩.该小汽车离家的距离s(千米)与时间t(时)的关系可以用图中的折线表示.根据图象提供的有关信息,解答下列问题:
“国庆黄金周”的某一天,小明全家上午8时自驾小汽车从家里出发,到距离180千米的某著名旅游景点游玩.该小汽车离家的距离s(千米)与时间t(时)的关系可以用图中的折线表示.根据图象提供的有关信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在直角坐标系中,每个小正方形的边长都是单位1.
如图,在直角坐标系中,每个小正方形的边长都是单位1.查看答案和解析>>
科目:初中数学 来源: 题型:
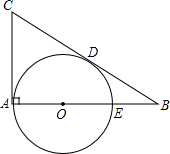 如图,在Rt△ABC中,∠BAC=90°,∠ABC=30°,Q是AB上的一点,⊙O分别与AC、BC相切于点A、D,与AB交于另一点E,若BE=2,则切线CD的长为( )
如图,在Rt△ABC中,∠BAC=90°,∠ABC=30°,Q是AB上的一点,⊙O分别与AC、BC相切于点A、D,与AB交于另一点E,若BE=2,则切线CD的长为( )A、
| ||
B、2
| ||
C、3
| ||
| D、6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com