
【题目】如图(1),△ABC是一个三角形的纸片,点D、E分别是△ABC边上的两点,
研究(1):如果沿直线DE折叠,则∠BDA′与∠A的关系是 .
研究(2):如果折成图2的形状,猜想∠BDA′、∠CEA′和∠A的关系,并说明理由.
研究(3):如果折成图3的形状,猜想∠BDA′、∠CEA′和∠A的关系,并说明理由.

【答案】(1)∠BDA′=2∠A;(2)∠BDA′+∠CEA′=2∠A;(3)∠BDA′-∠CEA′=2∠A
【解析】
试题分析:翻折问题要在图形是找着相等的量.图1中DE为折痕,有∠A=∠DA′A,再利用外角的性质可得结论∠BDA′=2∠A图2中∠A与∠DA′E是相等的,再结合四边形的内角和及互补角的性质可得结论∠BDA′+∠CEA′=2∠A图3中由于折叠∠A与∠DA′E是相等的,再两次运用三角形外角的性质可得结论.
试题解析:(1)∠BDA′=2∠A;
(2)∠BDA′+∠CEA′=2∠A,
理由:在四边形ADA′E中,∠A+∠DA′E+∠ADA′+∠A′EA=360°
∴∠A+∠DA′E=360°-∠ADA′-∠A′EA
∵∠BDA′+∠ADA′=180°,∠CEA′+∠A′EA=180°
∴∠BDA′+∠CEA′=360°-∠ADA′-∠A′EA
∴∠BDA′+∠CEA′=∠A+∠DA′E
∵△A′DE是由△ADE沿直线DE折叠而得
∴∠A=∠DA′E
∴∠BDA′+∠CEA′=2∠A;
(3)∠BDA′-∠CEA′=2∠A
理由:DA′交AC于点F,
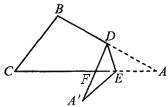
∵∠BDA′=∠A+∠DFA,∠DFA=∠A′+∠CEA′
∴∠BDA′=∠A+∠A′+∠CEA′
∴∠BDA′-∠CEA′=∠A+∠A′
∵△A′DE是由△ADE沿直线DE折叠而得
∴∠A=∠DA′E
∴∠BDA′-∠CEA′=2∠A.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】某校在一次考试中,甲,乙两班学生的数据成绩统计如下:
请根据表格提供的信息回答下列问题:
分数 | 50 | 60 | 70 | 80 | 90 | 100 | |
人数 | 甲 | 1 | 6 | 12 | 11 | 15 | 5 |
乙 | 3 | 5 | 15 | 3 | 13 | 11 | |
(1)甲班众数为 分,乙班众数为 分,从众数看成绩较好的是 班;
(2)甲班的中位数是 分,乙班的中位数是 分;
(3)若成绩在80分以上为优秀,则成绩较好的是 班;
(4)甲班的平均成绩是 分,乙班的平均成绩是 分,从平均分看成绩较好的是 班.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图甲是一个长为2m,宽为2n的长方形,沿图中的虚线剪成四个全等的小长方形,再按图乙围成一个较大的正方形.

(1)请用两种方法表示图中阴影部分面积(只需表示,不必化简);
(2)比较(1)两种结果,你能得到怎样的等量关系?
请你用(2)中得到等量关系解决下面问题:如果m﹣n=5,mn=14,求m+n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你能化简(x-1)(x99+x98+x97+……+x+1)吗?遇到这样的问题,我们可以先思考一下,从简单的情形入手.
分别计算下列各式的值:
①(x-1)(x+1)=x2-1;
②(x-1)(x2+x+1)=x3-1;;
③(x-1)(x3+x2+1)=x4-1;;……
由此我们可以得到:(x-1)(x99+x98+x97+…+x+1)=________________;
请你利用上面的结论,完成下面两题的计算,并写出计算过程:
(1) 299+298+297+……+2+1;
(2)(-2)50+(-2)49+(-2)48+……+(-2)+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).

(1)先将△ABC竖直向上平移6个单位,再水平向右平移1个单位得到△A1B1C1,请画出△A1B1C1;
(2)将△A1B1C1绕B1点顺时针旋转90°,得△A2B1C2,请画出△A2B1C2;
(3)求(2)中点A1旋转到点A2所经过的弧长![]() (结果保留π).
(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划开设4门选修课:音乐、绘画、体育、舞蹈,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门),对调查结果进行统计后,绘制了如下不完整的两个统计图.
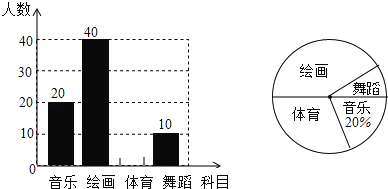
根据以上统计图提供的信息,回答下列问题:
(1)此次调查抽取的学生人数为a= 人,其中选择“绘画”的学生人数占抽样人数的百分比为b= ;
(2)补全条形统计图;
(3)若该校有2000名学生,请估计全校选择“绘画”的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
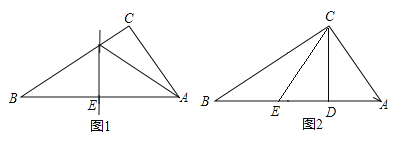
【题目】在数学实验课上,李静同学剪了两张直角三角形纸片,进行如下的操作:
操作一:如图1,将Rt△ABC纸片沿某条直线折叠,使斜边两个端点A与B重合,折痕为DE.
(1)如果AC=5cm,BC=7cm,可得△ACD的周长为 ;
(2)如果∠CAD:∠BAD=1:2,可得∠B的度数为 ;
操作二:如图2,李静拿出另一张Rt△ABC纸片,将直角边AC沿直线CD折叠,使点A与点E重合,若AB=10cm,BC=8cm,请求出BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com