
如图,已知⊙O是正方形ABCD的外接圆,点E是 上任意一点,则∠BEC 的度数为 ( )
上任意一点,则∠BEC 的度数为 ( )
A. 30° B. 45° C. 60° D. 90°
 |
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
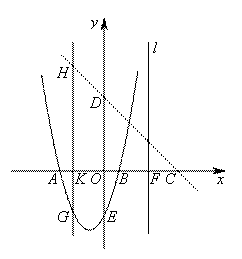
如图,抛物线y=ax2+bx+c交x轴于点A(-3,0),点B(1,0),交y轴于点E(0,-3).点C是点A关于点B的对称点,点F是线段BC的中点,直线l过点F且与y轴平行.直线y=-x+m过点C,交y轴于点D.
(1)求抛物线的解析式;
(2)点K为线段AB上一动点,过点K作x轴的垂线,交直线CD于点H,交抛物线于点G,求线段HG长度的最大值;
(3)在直线l上取点M,在抛物线上取点N,使以A,C,M,N为顶点的四边形是平行四边形,求点N的坐标.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,Rt△ABC的直角边BC在x轴正半轴上,点D为斜边AC的中点,DB的延长线交y轴负半轴于点E,反比例函数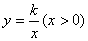 的图象经过点A.若S△BEC=4,则k的值
的图象经过点A.若S△BEC=4,则k的值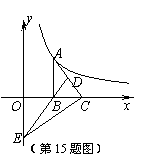 为 ;
为 ;
查看答案和解析>>
科目:初中数学 来源: 题型:
阅读理解:配方法是中学数学的重要方法,用配方法可求最大(小)值。
对于任意正实数a、b,可作如下变形a+b=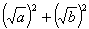 =
=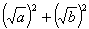 -
- +
+ =
= +
+  ,
,
又∵ ≥0, ∴
≥0, ∴ +
+  ≥0+
≥0+ ,即
,即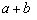 ≥
≥ .
.
(1)根据上述内容,回答下列问题:在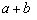 ≥
≥ (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥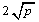 ,当且仅当a、b满足 时,a+b有最小值
,当且仅当a、b满足 时,a+b有最小值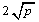 .
.
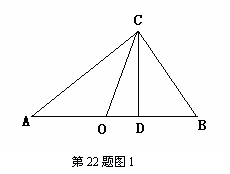
(2)思考验证:如图1,△ABC中,∠ACB=90°,CD⊥AB,垂足为D,CO为AB边上中线,AD=2a,DB=2b, 试根据图形验证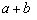 ≥
≥ 成立,并指出等号成立时的条件.
成立,并指出等号成立时的条件.
 (3)探索应用:如图2,已知A为反比例函数
(3)探索应用:如图2,已知A为反比例函数 的图像上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连结DF、EF,求四边形ADFE面积的最小值.
的图像上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连结DF、EF,求四边形ADFE面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
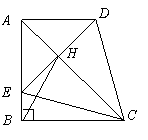
在直角梯形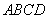 中,
中, ,
,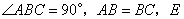 为
为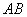 边上一点,
边上一点, ,且
,且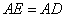 .连接
.连接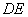 交对角线
交对角线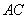 于
于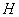 ,连接
,连接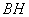 .下列结论:
.下列结论:
①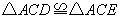 ;②
;②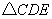 为等边三角形;③
为等边三角形;③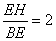 ; ④.
; ④.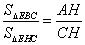
其中结论正确的是( )
A.只有①② B.只有①②④ C.只有③④ D.①②③④
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,A、M是反比例函数 的图象上的两点,过点M作直线MB∥x轴,交
的图象上的两点,过点M作直线MB∥x轴,交 轴于点B;过点
轴于点B;过点 作直线
作直线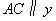 轴交
轴交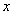 轴于点
轴于点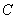 ,交直线MB于点D.BM:DM=8:9,当四边形OADM的面积为
,交直线MB于点D.BM:DM=8:9,当四边形OADM的面积为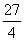 时,k= .
时,k= .
查看答案和解析>>
科目:初中数学 来源: 题型:
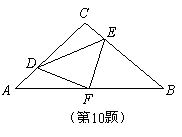
如图,在等腰 中,
中,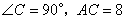 ,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持
,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持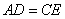 .连接DE、DF、EF.在此运动变化的过程中,下列结论:①
.连接DE、DF、EF.在此运动变化的过程中,下列结论:①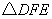 是等腰直角三角形;②四边形CDFE不可能为正方形,③DE长度的最小值为4;④四边形CDFE的面积保持不变;⑤△CDE面积的最大值为8.其中正确的结论是( )
是等腰直角三角形;②四边形CDFE不可能为正方形,③DE长度的最小值为4;④四边形CDFE的面积保持不变;⑤△CDE面积的最大值为8.其中正确的结论是( )
A.①④⑤ B.③④⑤ C.①③④ D.①②③


查看答案和解析>>
科目:初中数学 来源: 题型:
如图,函数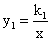 与
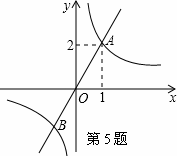
与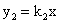 的图象相交于点A(1,2)和点B,当y1>y2时的变量x的取值范围是( )(原创)
的图象相交于点A(1,2)和点B,当y1>y2时的变量x的取值范围是( )(原创)
A、x>1 B、-1<x<0 C、-1<x<0或x>1 D、x<-1或0<x<1
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com