
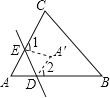
【题目】如图,小李制作了一张△ABC纸片,点D、E分别在边AB、AC上,现将△ABC沿着DE折叠压平,使点A落在点A′位置.若∠A=75°,则∠1+∠2= .
科目:初中数学 来源: 题型:
【题目】如图,在一棵树CD的10m高处的B点有两只猴子,它们都要到A处池塘边喝水,其中一只猴子沿树爬下走到离树20m处的池塘A处,另一只猴子爬到树顶D后直线跃入池塘的A处.如果两只猴子所经过的路程相等,试问这棵树多高?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,直线l为BC的中垂线,射线m为∠ABC的角平分线,直线l与m相交于点P.若∠BAC=60°,∠ACP=24°,则∠ABP的度数是( )

A. 24° B. 30° C. 32° D. 36°
查看答案和解析>>
科目:初中数学 来源: 题型:
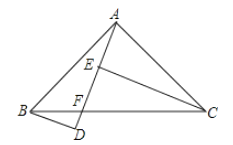
【题目】如图,![]() 中,∠BAC=90°,AB=AC,F是BC上一点,BD
中,∠BAC=90°,AB=AC,F是BC上一点,BD![]() AF的延长线与D,CE
AF的延长线与D,CE![]() AF于E,已知CE=5,BD=2,ED=__________
AF于E,已知CE=5,BD=2,ED=__________
查看答案和解析>>
科目:初中数学 来源: 题型:
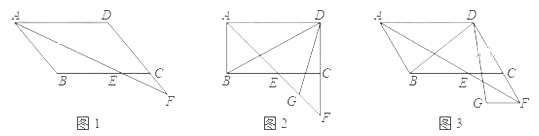
【题目】在平行四边形ABCD中,E是BC上任意一点,延长AE交DC的延长线与点F.
(1)在图中当CE=CF时,求证:AF是∠BAD的平分线.
(2)在(1)的条件下,若∠ABC=90°,G是EF的中点(如图),请求出∠BDG的度数.
(3)如图,在(1)的条件下,若∠BAD=60°,且FG∥CE,FG=CE,连接DB、DG,求出∠BDG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校在假期内对教室内的黑板进行整修,需在规定日期内完成,如果由甲工程小组做,恰好按期完成;如果由乙工程小组做,则要超过规定日期15天;如果两组合作了10天,余下部分由乙组独做,正好在规定日期内完成.
(1)这项工程的规定时间是多少天?
(2)已知甲组每天的施工费用为500元,乙组每天的施工费用为300元,为了缩短工期在假期内尽快完成任务,学校最终决定该工程由甲、乙两组合做来完成,那么该工程施工费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
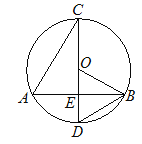
【题目】如图,CD为⊙O的直径,弦AB交CD于点E,连接BD、OB.
(1)求证:△AEC∽△DEB;
(2)若CD⊥AB,AB=8,DE=2,求⊙O的半径.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,过等边三角形ABC边AB上一点D作DE∥BC交边AC于点E,分别取BC,DE的中点M,N,连接MN.
(1)发现:在图1中,![]() ,说明理由;
,说明理由;
(2)探索:如图2,将△ADE绕点A旋转,请求出![]() 的值;
的值;
(3)拓展:如图3,△ABC和△ADE是等腰三角形,且∠BAC=∠DAE,M,N分别是底边BC,DF的中点,若BD⊥CE,请直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.
恒成立的结论有 .(把你认为正确的序号都填上)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com