
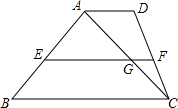
 在梯形ABCD中,AD∥BC,点E、F分别在边AB、CD上.EF∥BC,EF交AC于G.EB=DF,AE=9,CF=4.求BE,CD,$\frac{GF}{AD}$的值.
在梯形ABCD中,AD∥BC,点E、F分别在边AB、CD上.EF∥BC,EF交AC于G.EB=DF,AE=9,CF=4.求BE,CD,$\frac{GF}{AD}$的值. 分析 根据平行线分线段成比例得到$\frac{AE}{BE}=\frac{DF}{CF}$,由EB=DF,得到BE2=AE•CF=36,求得BE=DF=6,通过△CFG∽△CAD,即可得到结论.
解答 解:∵AD∥BC,EF∥BC,
∴$\frac{AE}{BE}=\frac{DF}{CF}$,
∵EB=DF,
∴BE2=AE•CF=36,
∴BE=DF=6,
∴CD=CF+DF=10,
∵GF∥AD,
∴△CFG∽△CAD,
∴$\frac{GF}{AD}=\frac{CF}{CD}$=$\frac{4}{10}$=$\frac{2}{5}$.
点评 本题考查了相似三角形的判定和性质,平行线分线段成比例,熟练掌握相似三角形的判定和性质是解题的关键.


科目:初中数学 来源: 题型:解答题
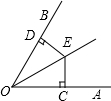 如图,E是∠AOB的角平分线上的一点,EC⊥OA,ED⊥OB,垂足分别为C,D,试说明
如图,E是∠AOB的角平分线上的一点,EC⊥OA,ED⊥OB,垂足分别为C,D,试说明查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
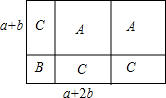 如图,有足够多的正方形(A型和B型)和长方形(C型)卡片,利用这些卡片可以进行因式分解,如对多项式2a2+3ab+b2进行因式分解.
如图,有足够多的正方形(A型和B型)和长方形(C型)卡片,利用这些卡片可以进行因式分解,如对多项式2a2+3ab+b2进行因式分解.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
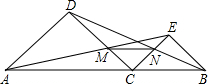 如图,点C在线段AB上(不与端点重合),点D、E在AB同侧,且AD∥CE,CD∥BE,连接AE交CD于M,连接BD交CE于N.
如图,点C在线段AB上(不与端点重合),点D、E在AB同侧,且AD∥CE,CD∥BE,连接AE交CD于M,连接BD交CE于N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
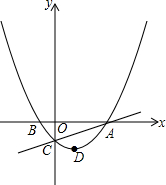 如图,已知抛物线y=$\frac{1}{3}$x2+$\frac{1}{3}$(b+1)x+$\frac{b}{3}$与x轴交于点A、B(点A位于点B的右侧),与y轴负半轴交于点C,顶点为D.
如图,已知抛物线y=$\frac{1}{3}$x2+$\frac{1}{3}$(b+1)x+$\frac{b}{3}$与x轴交于点A、B(点A位于点B的右侧),与y轴负半轴交于点C,顶点为D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
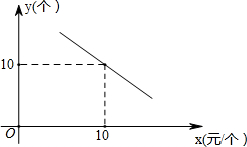 某文具店到批发市场选购A、B两种文具,批发价分别为14元/个、10元/个.若该店零售A、B两种文具的每天销量y(个)与零售价x(元/个)都是一次函数y=kx+20的关系,如图所示.
某文具店到批发市场选购A、B两种文具,批发价分别为14元/个、10元/个.若该店零售A、B两种文具的每天销量y(个)与零售价x(元/个)都是一次函数y=kx+20的关系,如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com