
【题目】如图,在平面直角坐标系中,Rt△ABC的顶点B在原点O,直角边BC在x轴的正半轴上,∠ACB=90°,点A的坐标为(3, ![]() ),点D是BC边上一个动点(不与点B,C重合),过点D作DE⊥BC交AB边于点E,将∠ABC沿直线DE翻折,点B落在x轴上的点F处当△AEF为直角三角形时,点F的坐标是 .
),点D是BC边上一个动点(不与点B,C重合),过点D作DE⊥BC交AB边于点E,将∠ABC沿直线DE翻折,点B落在x轴上的点F处当△AEF为直角三角形时,点F的坐标是 . 
【答案】(2,0)或(4,0)
【解析】解:①如图1中,当∠AFE=90°,
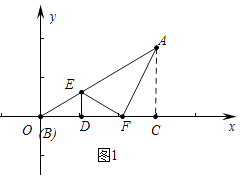
∵A(3, ![]() ),
),
∴OC=3,AC= ![]() ,
,
∴tan∠AOC= ![]() =
= ![]() ,
,
∴∠AOC=30°,
∵EO=EF,
∴∠EOF=∠EFO=30°,
∴∠AEF=∠EOF+∠EFO=60°,
∴∠EAF=∠FAC=30°,
∴CF=ACtan30°=1,
∴OF=OC﹣CF=2,
∴F(2,0).
②如图2中,当∠EAF=90°时,
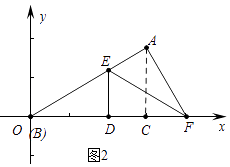
易知∠CAF=30°,
CF=ACtan30°=1,
∴OF=OC+CF=4,
∴F(4,0),
③∠AEF=60°,不可能为90°.
所以答案是:(2,0)或(4,0).
【考点精析】解答此题的关键在于理解锐角三角函数的定义的相关知识,掌握锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数,以及对特殊角的三角函数值的理解,了解分母口诀:30度、45度、60度的正弦值、余弦值的分母都是2,30度、45度、60度的正切值、余切值的分母都是3,分子口诀:“123,321,三九二十七”.


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3,点0是对角线AC,BD的交点,点E在CD上,且DE=2CE,连接BE.过点C作CF⊥BE,垂足为F,连接OF,则OF的长为 . 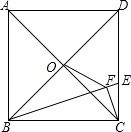
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠ACB=90°,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC.若点F是DE的中点,连接AF,则AF=( )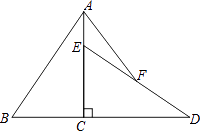
A.4
B.5
C.4 ![]()
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a,b在数轴上的对应点如图所示,则下列式子中错误的是( )
![]()
A. a+b<0 B. a-b<0
C. -a<-b D. |a-b|=b-a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1,可得AD平分∠BAC.
理由如下:∵AD⊥BC于D,EG⊥BC于G,(_______)
∴∠ADC=∠EGC=90°,(垂直的定义),
∴AD∥EG,(_______)
∴∠1=∠2,(_______)
∠E=∠3,(_______)
又∵∠E=∠1(已知),
∴______=_______,(______)
∴AD平分∠BAC.(_______)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图A在数轴上所对应的数为﹣2.
(1)点B在点A右边距A点4个单位长度,求点B所对应的数;
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点 B 以每秒2个单位长度沿数轴向右运动,当点A运动到﹣6所在的点处时,求A,B两点间距离.
(3)在(2)的条件下,现A点静止不动,B点再以每秒2个单位长度沿数轴向左运动时,经过多长时间A,B两点相距4个单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B,C,D为矩形的四个顶点,AB=16 cm,BC=6 cm,动点P,Q分别从点A,C同时出发,点P以3 cm/s的速度向点B移动,点Q以2 cm/s的速度向点D移动.当点P运动到点B停止时,点Q也随之停止运动.问几秒时点P和点Q的距离是10 cm?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D,E,F是垂足,且AB=5,BC=4,AC=3,则点O到三边AB,AC,BC的距离分别是( )
A. 1,1,1 B. 2,2,2 C. 1,1.5,2 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠C>∠B.如图①,AD⊥BC于点D,AE平分∠BAC.
(1)如图①,AD⊥BC于点D,AE平分∠BAC,能猜想出∠DAE与∠B、∠C之间的关系是什么?并说明理由.
(2)如图②,AE平分∠BAC,F为AE上的一点,且FD⊥BC于点D,这时∠EFD与∠B、∠C有何数量关系?请说明理由.
(3)如图③,AE平分∠BAC,F为AE延长线上的一点,FD⊥BC于点D,请你写出这时∠EFD与∠B、∠C之间的数量关系(只写结论,不必说明理由).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com