
【题目】某校为了体育活动更好的开展,决定购买一批篮球和足球.据了解:篮球的单价比足球的单价多20元,用1000元购买篮球的个数与用800元购买足球的个数相同.
(1)篮球、足球的单价各是多少元?
(2)若学校打算购买篮球和足球的数量共100个,且购买的总费用不超过9600元,问最多能购买多少个篮球?
科目:初中数学 来源: 题型:
【题目】两个工程队共同参与一项筑路工程,若先由甲、乙队合作![]() 天,剩下的工程再由乙队单独做
天,剩下的工程再由乙队单独做![]() 天可以完成,共需施工费810万元;若由甲、乙合作完成此项工程共需
天可以完成,共需施工费810万元;若由甲、乙合作完成此项工程共需![]() 天,共需施工费
天,共需施工费![]() 万元.
万元.
(1)求乙队单独完成这项工程需多少天?
(2)甲、乙两队每天的施工费各为多少万元?
(3)若工程预算的总费用不超过![]() 万元,则乙队最少施工多少天?
万元,则乙队最少施工多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
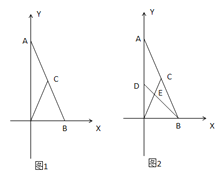
【题目】如图1,在平面直角坐标系中,已知点![]() ,点
,点![]() ,
,![]() 为线段
为线段![]() 上一点,且满足
上一点,且满足![]() .
.
(1)求直线![]() 的解析式及点
的解析式及点![]() 的坐标;
的坐标;
(2)如图2,![]() 为线段
为线段![]() 上一动点,连接
上一动点,连接![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,试探索
,试探索![]() 是否为定值?若是,求出该值;若不是,请说明理由;
是否为定值?若是,求出该值;若不是,请说明理由;
(3)点![]() 为坐标轴上一点,请直接写出满足
为坐标轴上一点,请直接写出满足![]() 为等腰三角形的所有点
为等腰三角形的所有点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
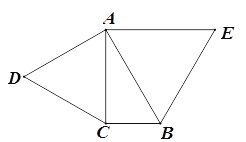
【题目】已知△ABC中, ∠ACB=90°,∠CAB=30°,以AC,AB为边向外作等边三角形ACD和等边三角形ABE,点F在AB上,且到AE,BE的距离相等.
(1)用尺规作出点F; (要求:尺规作图,保留作图痕迹,不写作法)
(2)连接EF,DF,证明四边形ADFE为平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读解答题:
(几何概型)
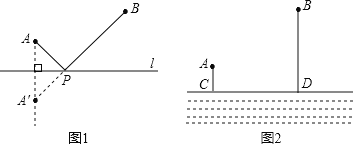
条件:如图1:![]() 是直线
是直线![]() 同旁的两个定点.
同旁的两个定点.
问题:在直线![]() 上确定一点
上确定一点![]() ,使
,使![]() 的值最小;
的值最小;
方法:作点![]() 关于直线
关于直线![]() 对称点
对称点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,则
,则![]() ,
,
由“两点之间,线段最短”可知,点![]() 即为所求的点.
即为所求的点.
(模型应用)
如图2所示:两村![]() 在一条河
在一条河![]() 的同侧,
的同侧,![]() 两村到河边
两村到河边![]() 的距离分别是
的距离分别是![]() 千米,
千米,![]() 千米,
千米, ![]() 千米,现要在河边
千米,现要在河边![]() 上建造一水厂,向
上建造一水厂,向![]() 两村送水,铺设水管的工程费用为每千米20000元,请你在
两村送水,铺设水管的工程费用为每千米20000元,请你在![]() 上选择水厂位置,使铺设水管的费用最省,并求出最省的铺设水管的费用
上选择水厂位置,使铺设水管的费用最省,并求出最省的铺设水管的费用![]() .
.
(拓展延伸)
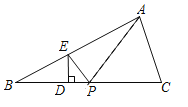
如图,![]() 中,点
中,点![]() 在边
在边![]() 上,过
上,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,
,![]() 为
为![]() 上一个动点,连接
上一个动点,连接![]() ,若
,若![]() 最小,则点
最小,则点![]() 应该满足( )(唯一选项正确)
应该满足( )(唯一选项正确)
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,点
中,点![]() 为
为![]() 边中点,点
边中点,点![]() 为
为![]() 边中点;点
边中点;点![]() ,
, ![]() 为
为![]() 边三等分点,
边三等分点, ![]() ,
, ![]() 为
为![]() 边三等分点.小瑞分别用不同的方式连接矩形对边上的点,如图2,图3所示.那么,图2中四边形
边三等分点.小瑞分别用不同的方式连接矩形对边上的点,如图2,图3所示.那么,图2中四边形![]() 的面积与图3中四边形
的面积与图3中四边形![]() 的面积相等吗?
的面积相等吗?
(1)小瑞的探究过程如下
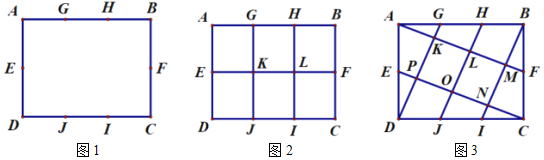
在图2中,小瑞发现, ![]() ;
;
在图3中,小瑞对四边形![]() 面积的探究如下. 请你将小瑞的思路填写完整:
面积的探究如下. 请你将小瑞的思路填写完整:
设![]() ,
, ![]()
∵![]()
∴![]() ,且相似比为
,且相似比为![]() ,得到
,得到![]()
∵![]()
∴![]() ,且相似比为
,且相似比为![]() ,得到
,得到![]()
又∵![]() ,
, ![]()
∴![]()
∴![]() ,
, ![]() ,
, ![]()
∴![]() ,则
,则![]() (填写“
(填写“![]() ”,“
”,“![]() ”或“
”或“![]() ”)
”)
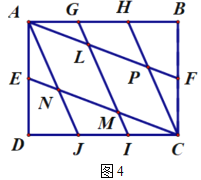
(2)小瑞又按照图4的方式连接矩形![]() 对边上的点.则
对边上的点.则![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
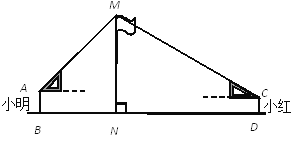
【题目】如图,在活动课上,小明和小红合作用一副三角板来测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,他调整自己的位置,设法使得三角板的一条直角边保持水平,且斜边与旗杆顶端M在同一条直线上,测得旗杆顶端M仰角为45°;小红的眼睛与地面的距离(CD)是1.5m,用同样的方法测得旗杆顶端M的仰角为30°.两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).求出旗杆MN的高度.(参考数据: ![]() ,结果保留整数.)
,结果保留整数.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习轴对称的时候,老师让同学们思考课本中的探究题.
如图(1),要在燃气管道l上修建一个泵站,分别向A、B两镇供气.泵站修在管道的什么地方,可使所用的输气管线最短?
你可以在l上找几个点试一试,能发现什么规律?你可以在![]() 上找几个点试一试,能发现什么规律?
上找几个点试一试,能发现什么规律?
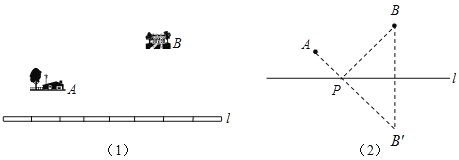
聪明的小华通过独立思考,很快得出了解决这个问题的正确办法.他把管道l看成一条直线(图(2)),问题就转化为,要在直线l上找一点P,使AP与BP的和最小.他的做法是这样的:
①作点B关于直线l的对称点B′.
②连接AB′交直线l于点P,则点P为所求.
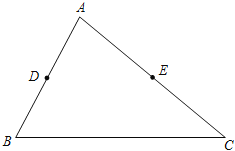
请你参考小华的做法解决下列问题.如图在△ABC中,点D、E分别是AB、AC边的中点,BC=6,BC边上的高为4,请你在BC边上确定一点P,使△PDE得周长最小.
(1)在图中作出点P(保留作图痕迹,不写作法).
(2)请直接写出△PDE周长的最小值:
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com