练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

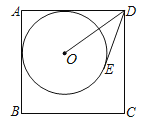
    【题目】如图，⊙O与正方形ABCD的两边AB，AD相切，且DE与⊙O相切于点E．若AB＝7，DO＝5，则DE的长度为_____．

    【答案】4或3

    【解析】

    设⊙O与AB、AD分别切于M、N两点，连接OM、ON，则可证得四边形AMON为正方形，利用切线长定理可求得DN=DE，设AN=x，则可得x2+(7﹣x)2=52，则可求得AN，则可求得DE．

    设⊙O与AB、AD分别切于M、N两点，连接OM、ON，

    ∵四边形ABCD为正方形，

    ∴∠A=90°，AD=AB=7，

    ∵AD、AB与⊙O相切，

    ∴∠ANO=∠AMO=∠A=90°，且AM=AN，

    ∴四边形AMON为正方形，

    设AN=x，

    ∵ON2+DN2=OD2，

    ∴，

    解得=3或4，

    ∴AN=3或4，

    ∵DE与⊙O相切，

    ∴DN=DE=4或3，

    故答案为：4或3．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】跳绳是大家喜闻乐见的一项体育运动，集体跳绳时，需要两人同频甩动绳子，当绳子甩到最高处时，其形状可近似看作抛物线.如图是小明和小亮甩绳子到最高处时的示意图，两人拿绳子的手之间的距离为，离地面的高度为，以小明的手所在位置为原点，建立平面直角坐标系.

    （1）当身高为的小红站在绳子的正下方，且距小明拿绳子手的右侧处时，绳子刚好通过小红的头顶，求绳子所对应的抛物线的表达式；

    （2）若身高为的小丽也站在绳子的正下方.

    ①当小丽在距小亮拿绳子手的左侧处时，绳子能碰到小丽的头吗？请说明理由；

    ③设小丽与小亮拿绳子手之间的水平距离为，为保证绳子不碰到小丽的头顶，求的取值范围.（参考数据：取3.16）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形中，，为边的中点，将绕点顺时针旋转，点的对应点为，点的对应点为，过点作交于点，连接、交于点，现有下列结论：①；②；③；④点为的外心．其中正确的是（ ）

    A.①④B.①③C.③④D.②④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB＝90°，AC＝BC＝4cm，点P从点A出发以lcm/s的速度沿折线AC﹣CB运动，过点P作PQ⊥AB于点Q，当点P不与点A、B重合时，以线段PQ为边向右作正方形PQRS，设正方形PQRS与△ABC的重叠部分面积为S，点P的运动时间为t（s）．

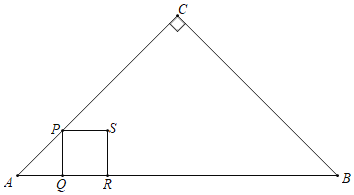
    （1）用含t的代数式表示CP的长度；

    （2）当点S落在BC边上时，求t的值；

    （3）当正方形PQRS与△ABC的重叠部分不是五边形时，求S与t之间的函数关系式；

    （4）连结CS，当直线CS分△ABC两部分的面积比为1：2时，直接写出t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】武汉市政府大力扶持大学生创业，童威在政府的扶持下投资销售一种进价为每盏20元的护眼台灯，销售过程中发现，每月销售量y（盏）与销售单价x（元）之间的关系可近似地看作一次函数：y＝﹣10x+500．

    （1）设每月获得的利润为w（元），求w与x的关系式．

    （2）如果想要每月获得2000元的利润，那么销售单价应定为多少元？

    （3）根据物价部门规定，这种护眼台灯的销售单价不得高于32元．如果童威想要每月获得的利润不低于2000元，那么他每月的成本最少需要多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，△ABC中，AC＝BC，∠ACB＝90°，点P为AB上一点（异于A、B），BD⊥直线CP于D，AE⊥直线CP于E，点F为AB的中点，连接DF．

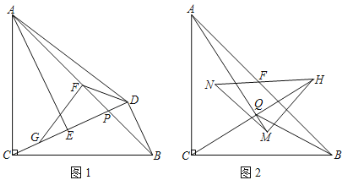
    （1）可以把△ACE绕点F逆时针旋转　 　度（度数不超过180°）和△　 　重合，则∠FDE＝　 　°．

    （2）取CE的中点G，连接AD、FG，求证：AD＝2FG．

    （3）如图2，AB＝8，等腰直角△MNH的斜边NH的中点也为点F，直线AM和直线CH交于点Q，连接BQ，当△MNH绕点F旋转一周时，请直接写出BQ长的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

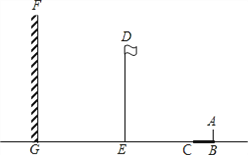
    【题目】如图，阳光下，小亮的身高如图中线段AB所示，他在地面上的影子如图中线段BC所示，线段DE表示旗杆的高，线段FG表示一堵高墙．

    （1）请你在图中画出旗杆在同一时刻阳光照射下形成的影子，并用线段表示；

    （2）如果小亮的身高AB=1.6m，他的影子BC=2.4m，旗杆的高DE=15m，旗杆与高墙的距离EG=16m，请求出旗杆的影子落在墙上的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某水果经销商到水果种植基地采购葡萄，经销商一次性采购葡萄的采购单价（元/千克）与采购量（千克）之间的函数关系图象如图中折线所示（不包括端点）.

    （1）当时，写出与之间的函数关系式；

    （2）葡萄的种植成本为8元/千克，某经销商一次性采购葡萄的采购量不超过1000千克，当采购量是多少时，水果种植基地获利最大，最大利润是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，∠AOB＝90°，OA＝4，OB＝3，点E在线段OA上，EP⊥OA交AB于点N，PM⊥AB，直线PB与AO交于点F．

    （1）若AN＝3，S△PBN＝8，求PN的长；

    （2）设△PMN的周长为C1，△AEN的周长为C2，若△PFE～△BAO且＝，求OE的长；

    （3）如图2，若OE＝2，将线段OE绕点O逆时针旋转得到OE'，旋转角为α （0°＜α＜90°），连接E'A、E'B，求E'A+E'B的最小值．

    查看答案和解析>>

    同步练习册答案