
【题目】在平面直角坐标系中,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() ,交
,交![]() 轴于点
轴于点![]() ,点
,点![]() 抛物线的顶点,对称轴与
抛物线的顶点,对称轴与![]() 轴交于点
轴交于点![]() .
.
⑴.求抛物线的解析式;
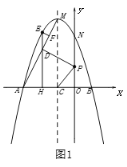
⑵.如图1,连接![]() ,点
,点![]() 是线段
是线段![]() 上方抛物线上的一动点,
上方抛物线上的一动点,![]() 于点
于点![]() ;过点
;过点![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() .点
.点![]() 是
是![]() 轴上一动点,当
轴上一动点,当![]() 取最大值时.
取最大值时.
①.求![]() 的最小值;
的最小值;
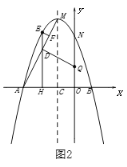
②.如图2,![]() 点是
点是![]() 轴上一动点,请直接写出
轴上一动点,请直接写出![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]()
【解析】
(1)直接利用待定系数法,把A,B两点代入解析式即可求出.
(2)利用配方法求出M点,求出直线AM的解析式,从而可以得出经过点E且与直线AM平行的直线![]() 解析式,再根据当直线
解析式,再根据当直线![]() 与抛物线只有一个交点时,EF取最大值,利用根的判别式可求出E点和D点的坐标,再根据当P,B,D三点共线时,PD+PC有最小值,利用勾股定理即可求出.
与抛物线只有一个交点时,EF取最大值,利用根的判别式可求出E点和D点的坐标,再根据当P,B,D三点共线时,PD+PC有最小值,利用勾股定理即可求出.
(3)利用添加辅助线,对线段OQ进行转化,再根据三点共线求出最小值.
1)将A(-3,0)、B(1,0)代入二次函数![]() 得,
得,
![]() 解之得
解之得![]() ,∴二次函数的解析式为
,∴二次函数的解析式为![]() ;
;
(2)①将二次函数![]() 配方得
配方得![]() ,
,
∴M(-1,4)
设直线AM的解析式为![]() ,将
,将![]() 代入直线可得,
代入直线可得,
![]() 解得
解得![]() ,
,
∴直线AM的解析式为![]() ,
,
过E作直线![]() ,平行于直线AM,且解析式为
,平行于直线AM,且解析式为![]() ,
,
∵E在直线AM上方的抛物线上,
∴![]() ;
;
当直线![]() 与AM距离最大时,EF取得最大值,
与AM距离最大时,EF取得最大值,
∴当![]() 与抛物线只有一个交点时,EF取得最大值,
与抛物线只有一个交点时,EF取得最大值,
将直线![]() 的解析式代入抛物线得
的解析式代入抛物线得![]() ,
,
由题意可得,△=![]() ,经计算得
,经计算得![]() ,将
,将![]() 代入二次方程可得,
代入二次方程可得,
![]() ,
,
∴![]() ,即E点的横坐标为-2,将
,即E点的横坐标为-2,将![]() 代入抛物线得
代入抛物线得![]() ,
,
∴![]() ,
,
又∵![]() ⊥
⊥![]() 轴,
轴,
∴![]() ,将
,将![]() 代入直线AM,
代入直线AM,
∴![]() ,
,
∵![]() ,
,
∴B、C两点关于![]() 轴对称,
轴对称,
∴![]() ,
,
∴![]() ,当P、B、D三点不共线时
,当P、B、D三点不共线时![]() ,
,
当P、B、D三点共线时,![]() ,
,
∴当P、B、D三点共线时PC+PD取得最小值,
在Rt△BHD中。DH=2,BH=3,∴BD=![]() ,
,
∴![]() 的最小值为
的最小值为![]() ;
;
②过Q作直线平行于![]() 轴,并在
轴,并在![]() 轴右侧该直线上取一点G,使得,
轴右侧该直线上取一点G,使得,
QG=![]() ,
,
∴![]() ,当
,当![]() 三点共线时,
三点共线时,
DQ+QG取得最小值,设Q(0,y),则![]() ,
,
∵QG∥![]() 轴,
轴,
∴![]() ,
,
∴![]() ,
,
∴![]() 的最小值为
的最小值为![]() .
.
【点晴】
本题主要考查了二次函数综合应用,利用待定系数求解析式,根的判别式求点的坐标,利用三点共线求最值的问题.


科目:初中数学 来源: 题型:
【题目】如图,△OAC和△BAD都是等腰直角三角形,![]() ,反比例函数
,反比例函数![]() 在第一象限的图象经过点B,则S△OAC-S△BAD=( )
在第一象限的图象经过点B,则S△OAC-S△BAD=( )
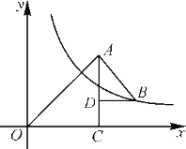
A.1.5B.2.5C.3D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,P是对角线BD上的一点,过点C作CQ∥DB,且CQ=DP,连接AP、BQ、PQ.
(1)求证:△APD≌△BQC;
(2)若∠ABP+∠BQC=180°,求证:四边形ABQP为菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某小型汽车的侧面示意图,其中矩形ABCD表示该车的后备箱,在打开后备箱的过程中,箱盖ADE可以绕点A逆时针方向旋转,当旋转角是50度时,箱盖落在![]() 的位置(如图2),已知
的位置(如图2),已知![]()
![]()
![]()
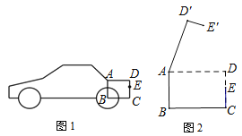
(1)求点![]() 到
到![]() 的距离;(结果保留整数)
的距离;(结果保留整数)
(2)求![]() 两点之间的距离.(结果保留整数)
两点之间的距离.(结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
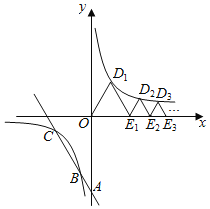
【题目】如图, 直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与双曲线
,与双曲线![]() 在第三象限交于
在第三象限交于![]() 两点,且
两点,且 ![]() ;下列等边三角形
;下列等边三角形![]() ,
,![]() ,
,![]() ,……的边
,……的边![]() ,
,![]() ,
,![]() ,……在
,……在![]() 轴上,顶点
轴上,顶点![]() ……在该双曲线第一象限的分支上,则
……在该双曲线第一象限的分支上,则![]() = ____,前25个等边三角形的周长之和为 _______.
= ____,前25个等边三角形的周长之和为 _______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料解答下列问题
观察下列方程:①![]() ,②
,②![]() ,③
,③![]() ……
……
⑴按此规律写出关于x的第n个方程为____________________,此方程的解为____________.
⑵根据上述结论,求出![]() 的解.
的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“微信运动”被越来越多的人关注和喜爱,某数学兴趣小组随机调查了我区50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数 | 频数 | 频率 |
0≤x<4000 | 8 | 0.16 |
4000≤x<8000 | 15 | 0.3 |
8000≤x<12000 | 12 | a |
12000≤x<16000 | b | 0.2 |
16000≤x<20000 | 3 | 0.06 |
20000≤x<24000 | 2 | 0.04 |
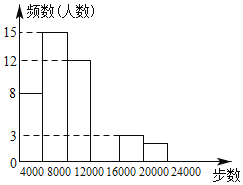
请根据以上信息,解答下列问题:
(1)写出a,b的值并补全频数分布直方图;
(2)我市约有5000名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?
(3)若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步)的两名教师与大家分享心得,用树形图或列表法求被选取的两名教师恰好都在20000步(包含20000步)以上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据调查:超速行驶是引发交通事故的主要原因之一.小明用所学知识对一条笔直公路上车辆进行测速,如图所示,观测点C到公路的距离CD=200m,检测路段的起点A位于点C的南偏东60°方向上,终点B位于点C的南偏东45°方向上,一辆轿车由东向西匀速行驶,测得此车由A处行驶到B处时的时间为10s,问此车是否超过了该路段10m/s的限制速度?(观测点C离地面的距离忽略不计,参专数据:![]() 1.41,
1.41,![]() 1.73)
1.73)
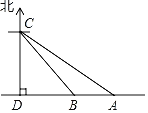
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O在![]() 的边
的边![]() 上,以
上,以![]() 为半径作
为半径作![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 于点D,过点D作
于点D,过点D作![]() 于点E.
于点E.
(1)尺规作图(不写作法,保留作图痕迹),补全图形;
(2)判断![]() 与
与![]() 交点的个数,并说明理由.
交点的个数,并说明理由.
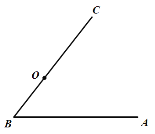
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com