

分析 (1)利用待定系数法求两个函数的解析式;
(2)根据总投资成本为10万元,设种植桃树的投资成本x万元,总利润为W万元,则种植柏树的投资成本(10-x)万元,列函数关系式,发现是二次函数,画出函数图象,找出当2≤x≤8时的最小利润和最大利润.
解答 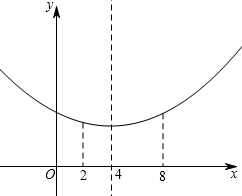 解:(1)把(4,1)代入y1=ax2中得:
解:(1)把(4,1)代入y1=ax2中得:
16a=1,
a=$\frac{1}{16}$,
∴y1=$\frac{1}{16}$x2,
把(2,1)代入y2=kx中得:
2k=1,
k=$\frac{1}{2}$,
∴y2=$\frac{1}{2}$x;
(2)设种植桃树的投资成本x万元,总利润为W万元,则种植柏树的投资成本(10-x)万元,
则W=y1+y2=$\frac{1}{16}$x2+$\frac{1}{2}$(10-x)=$\frac{1}{16}$(x-4)2+4,
由图象得:当2≤x≤8时,当x=4时,W有最小值,W小=4,
当x=8时,W有最大值,W大=$\frac{1}{16}$(8-4)2+4=5,
答:苗圃至少获得4万元利润,最多能获得5万元利润.
点评 本题是二次函数和一次函数的应用,考查了利用待定系数法求函数的解析式;对于二次函数,在求最值问题时,不一定都是顶点坐标,要根据实际情况和图象结合考虑,得出结论.


科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AC=BC,∠ACB=90°,点D,E在AB上,将△ACD,△BCE分别沿CD,CE翻折,点A,B分别落在点A′,B′的位置,再将△A′CD,△B′CE分别沿A′C,B′C翻折,点D与点E恰好重合于点O,则∠A′CB′的度数是( )
如图,在△ABC中,AC=BC,∠ACB=90°,点D,E在AB上,将△ACD,△BCE分别沿CD,CE翻折,点A,B分别落在点A′,B′的位置,再将△A′CD,△B′CE分别沿A′C,B′C翻折,点D与点E恰好重合于点O,则∠A′CB′的度数是( )| A. | 60° | B. | 45° | C. | 30° | D. | 15° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲 | B. | 乙 | C. | 甲、乙一样稳定 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 将正整数按如图所示的规律排列下去,若用有序实数对(n,m)表示第n排,从左到右第m个数,如(4,3)表示实数9,则(11,5)表示的实数是60.
将正整数按如图所示的规律排列下去,若用有序实数对(n,m)表示第n排,从左到右第m个数,如(4,3)表示实数9,则(11,5)表示的实数是60.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com