
【题目】如图22,在∠AOB的两边OA,OB上分别取OM=ON,OD=OE,DN和EM相交于点C.求证:点C在∠AOB的平分线上.
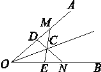
【答案】见解析
【解析】
过点C分别作CG⊥OA于点G,CF⊥OB于点F,在△MOE和△NOD中,根据OM=ON,∠MOE=∠NOD,OE=OD,可判定△MOE≌△NOD,根据全等三角形的性质可得:S△MOE=S△NOD,继而可得S△MOE-S四边形ODCE=S△NOD-S四边形ODCE,即S△MDC=S△NEC.
由三角形面积公式得DM·CG=EN·CF.由于OM=ON,OD=OE,所以DM=EN,CG=CF.
根据CG⊥OA,CF⊥OB,可证点C在∠AOB的平分线上.
证明:过点C分别作CG⊥OA于点G,CF⊥OB于点F,
如图.

在△MOE和△NOD中,OM=ON,∠MOE=∠NOD,OE=OD,
∴△MOE≌△NOD(SAS),
∴S△MOE=S△NOD,
∴S△MOE-S四边形ODCE=S△NOD-S四边形ODCE,
即S△MDC=S△NEC.
由三角形面积公式得DM·CG=EN·CF.
∵OM=ON,OD=OE,
∴DM=EN,
∴CG=CF.
又∵CG⊥OA,CF⊥OB,
∴点C在∠AOB的平分线上.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知:在平行四边形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF,且EG平分∠HEF.求证: 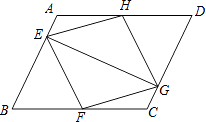
(1)△AEH≌△CGF;
(2)四边形EFGH是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y= ![]() 的图象经过点A(﹣
的图象经过点A(﹣ ![]() ,1).
,1).
(1)试确定此反比例函数的解析式;
(2)点O是坐标原点,将线段OA绕O点顺时针旋转30°得到线段OB.判断点B是否在此反比例函数的图象上,并说明理由;
(3)已知点P(m, ![]() m+6)也在此反比例函数的图象上(其中m<0),过P点作x轴的垂线,交x轴于点M.若线段PM上存在一点Q,使得△OQM的面积是
m+6)也在此反比例函数的图象上(其中m<0),过P点作x轴的垂线,交x轴于点M.若线段PM上存在一点Q,使得△OQM的面积是 ![]() ,设Q点的纵坐标为n,求n2﹣2
,设Q点的纵坐标为n,求n2﹣2 ![]() n+9的值.
n+9的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在热气球上A处测得塔顶B的仰角为52°,测得塔底C的俯角为45°,已知A处距地面98米,求塔高BC.(结果精确到0.1米)
【参考数据:sin52°=0.79,cos52°=0.62,tan52°=1.28】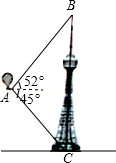
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上三点A,O,B对应的数分别为﹣5,0,1,点M为数轴上任意一点,其对应的数为x.
请回答问题:
![]()
(1)A、B两点间的距离是_____,若点M到点A、点B的距离相等,那么x的值是_____;
(2)若点A先沿着数轴向右移动6个单位长度,再向左移动4个单位长度后所对应的数字是 ____ ;
(3)当x为何值时,点M到点A、点B的距离之和是8;
(4)如果点M以每秒3个单位长度的速度从点O向左运动时,点A和点B分别以每秒1个单位长度和每秒4个单位长度的速度也向左运动,且三点同时出发,那么几秒种后点M运动到点A、点B之间,且点M到点A、点B的距离相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A的坐标为(0,3),点B的坐标为(4,0),C为第一象限内一点,AC⊥y轴,BC⊥x轴,D坐标为(m,0)(0<m<4).
(1)若D为OB的中点,求直线DC的解析式;
(2)若△ACD为等腰三角形,求m的值;
(3)E为四边形OACB的某一边上一点.
①若E在边BC上,满足△AOD≌△DBE,求m的值;
②若使△EOD为等腰三角形的点E有且只有4个,直接写出符合条件的m的值.
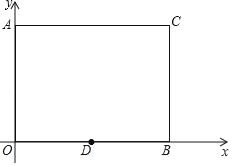
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com