
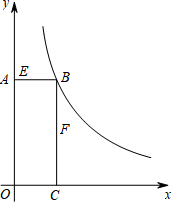
 如图,矩形AOCB的顶点B在反比例函数$y=\frac{k}{x}(k>0$,x>0)的图象上,且AB=3,BC=8.若动点E从A开始沿AB向B以每秒1个单位长度的速度运动,同时动点F从B开始沿BC向C以每秒2个单位长度的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动,设运动时间为t秒.
如图,矩形AOCB的顶点B在反比例函数$y=\frac{k}{x}(k>0$,x>0)的图象上,且AB=3,BC=8.若动点E从A开始沿AB向B以每秒1个单位长度的速度运动,同时动点F从B开始沿BC向C以每秒2个单位长度的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动,设运动时间为t秒.分析 (1)根据AB与BC的长,且B为第一象限角,确定出B的坐标,代入反比例函数解析式求出k的值,即可确定出反比例解析式;
(2)运动1秒时,在y轴上存在点D,使△DEF的周长最小,理由为:作出E关于y轴的对称点E′,连接E′F,与y轴交于点D,连接DE,EF,此时△DEF周长最小,求出周长最小值即可;
(3)存在,若四变形BEMF为平行四边形,则有三种可能,已知E(t,8),F(3,8-2t),0<t≤3.
①BE∥FM,此时M在F右侧,$M({\frac{24}{8-2t},8-2t})$,结合BE=FM,列出关于t的方程,解方程即可;
②BF∥EM,此时M在E正上方,$Mt({t,\frac{24}{t}})$,结合ME=BF,列出关于t的方程,解方程即可;
③EF∥BM,易知点M一定不在反比例函数上.
解答 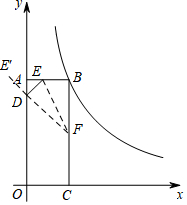 解:(1)由题可知点B的坐标为(3,8),且点B在$y=\frac{k}{x}$上.
解:(1)由题可知点B的坐标为(3,8),且点B在$y=\frac{k}{x}$上.
∴k=3×8=24,
∴反比例函数的表达式为:$y=\frac{24}{x}$.
(2)t=1时,E(1,8),F(3,6),则$EF=2\sqrt{2}$,
取E关于y轴的对称E′(-1,8),
连接E′F,${E^′}F=2\sqrt{5}$,${C_{△DEF}}=DE+DF+EF=2\sqrt{2}+D{E^′}+DF≥2G+{E^′}F$,
∴${C_{△DEFmin}}=2\sqrt{2}+2\sqrt{5}$,
此时点D为E′F与y轴交点,
∵E′(-1,8),F(3,6),
设E′F:y=kx+b,
则$\left\{\begin{array}{l}-k+b=8\\ 3k+b=6\end{array}\right.$,
解得$\left\{\begin{array}{l}k=-\frac{1}{2}\\ b=\frac{15}{2}\end{array}\right.$,
∴${E^′}F:y=\frac{1}{2}x+\frac{15}{2}$,
∴此时$D({0,\frac{15}{2}})$,
即:y轴上存在点$D({0,\frac{15}{2}})$,使△DEF的图长数小,且最小值为$2\sqrt{2}+2\sqrt{5}$.
(3)存在,若四变形BEMF为平行四边形,则有三种可能,已知E(t,8),F(3,8-2t),0<t≤3.
①BE∥FM,此时M在F右侧,$M({\frac{24}{8-2t},8-2t})$,
又∵BE=FM,
∴$3-t=\frac{24}{8-2t}-3$,t2-10t+12=0,
解得${t_1}=5-\sqrt{13}$,${t_2}=5+\sqrt{13}$(舍).
②BF∥EM,此时M在E正上方,$Mt({t,\frac{24}{t}})$,
∵ME=BF,
∴$\frac{24}{t}-8=2t$,t2+4t-12=0,
解得t1=2,t2=-6(舍).
③EF∥BM,易知点M一定不在反比例函数上,
故综上:t=2或$5-\sqrt{13}$.
点评 此题属于反比例函数综合题,涉及的知识有:待定系数法确定反比例函数解析式,坐标与图形性质,平行四边形的性质,熟练掌握性质及定理是解本题的关键.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A、B在⊙O上,点C在⊙O外,连接AB和OC交于D,且OB⊥OC,AC=CD.
如图,点A、B在⊙O上,点C在⊙O外,连接AB和OC交于D,且OB⊥OC,AC=CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了解今年全县2000名初二学生“创新能力大赛”的笔试情况,随机抽取了部分同学的成绩,整理并制作如图所示的图表(部分未完成).请你根据提供的信息,解答下列问题:
为了解今年全县2000名初二学生“创新能力大赛”的笔试情况,随机抽取了部分同学的成绩,整理并制作如图所示的图表(部分未完成).请你根据提供的信息,解答下列问题:| 分数段 | 频数 | 频率 |
| 60≤x<70 | 40 | 0.1 |
| 70≤x≤80 | 120 | n |
| 80≤x<90 | m | h |
| 90≤x<100 | 80 | 0.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com