
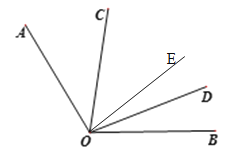
【题目】如图,已知∠AOB=α°,∠COD在∠AOB内部且∠COD=β°.
(1)若α,β满足|α-2β|+(β-60)2=0,则①α= ;
②试通过计算说明∠AOD与∠COB有何特殊关系;
(2)在(1)的条件下,如果作OE平分∠BOC,请求出∠AOC与∠DOE的数量关系;
(3)若α°,β°互补,作∠AOC,∠DOB的平分线OM,ON,试判断OM与ON的位置关系,并说明理由.

【答案】(1)①α=120;②∠AOD与∠COB互补,理由见解析;(2)∠DOE=![]() ∠AOC,理由见解析;(3)OM⊥ON,理由见解析.
∠AOC,理由见解析;(3)OM⊥ON,理由见解析.
【解析】
(1)①根据非负数的性质即可得出结论;
②先表示出∠AOD=∠AOB-∠DOB=120°-∠DOB,∠COB=∠COB+∠DOB=60°+∠DOB,即可得到结论;
(2)根据角的和差以及角平分线的性质计算即可;
(3)根据角的和差、角平分线的性质以及互补的概念计算即可.
(1)①由题意得:α-2β=0,β=60°,解得:α=120°;
②∵∠AOB=α°=120°,∠COD=β°=60°,
∴∠AOD=∠AOB-∠DOB=120°-∠DOB,∠COB=∠COB+∠DOB=60°+∠DOB,∴∠AOD+∠COB=180°,即∠AOD与∠COB互补;
(2)设∠AOC=θ,则∠BOC=120°-θ.
∵OE平分∠BOC,∴∠COE=![]() ∠BOC=
∠BOC=![]() (120°-θ)=60°-
(120°-θ)=60°-![]() θ,
θ,
∴∠DOE=∠COD-∠COE=60°-60°+![]() θ=
θ=![]() θ=
θ=![]() ∠AOC;
∠AOC;
(3)OM⊥ON.理由如下:
∵OM,ON分别平分∠AOC,∠DOB,
∴∠COM=![]() ∠AOC,
∠AOC,
∴∠DON=![]() ∠BOD,
∠BOD,
∴∠MON=∠COM+∠COD+∠DON
=![]() ∠AOC+
∠AOC+![]() ∠BOD+∠COD
∠BOD+∠COD
=![]() (∠AOC+∠BOD)+∠COD
(∠AOC+∠BOD)+∠COD
=![]() (∠AOB-∠COD)+∠COD
(∠AOB-∠COD)+∠COD
=![]() (∠AOB+∠COD)
(∠AOB+∠COD)
=![]() (α°+β°)
(α°+β°)
∵α°,β°互补,
∴α°+β°=180°,
∴∠MON=90°,
∴OM⊥ON.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的AC边在直线m上,∠ACB=80°,以C为圆心, ![]() BC长为半径画弧,交直线m于点D1、交BC于点E1 , 连接D1E1;又以D1为圆心,
BC长为半径画弧,交直线m于点D1、交BC于点E1 , 连接D1E1;又以D1为圆心, ![]() D1E1长为半径画弧,交直线m于点D2、交D1E1于点E2 , 连接D2E2;又以D2为圆心,
D1E1长为半径画弧,交直线m于点D2、交D1E1于点E2 , 连接D2E2;又以D2为圆心, ![]() D2E2长为半径画弧,交直线m于点D3、交D2E2于点E3 , 连接D3E3;如此依次下去,…,第n次时所得的∠EnDnDn﹣1= .
D2E2长为半径画弧,交直线m于点D3、交D2E2于点E3 , 连接D3E3;如此依次下去,…,第n次时所得的∠EnDnDn﹣1= . 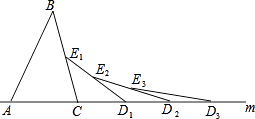
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是初三某班女生的体重检查结果:
体重(kg) | 34 | 35 | 38 | 40 | 42 | 45 | 50 |
人数 | 1 | 2 | 5 | 5 | 4 | 2 | 1 |
根据表中信息,回答下列问题:
(1)该班女生体重的中位数是;
(2)该班女生的平均体重是kg;
(3)根据上表中的数据补全条形统计图. 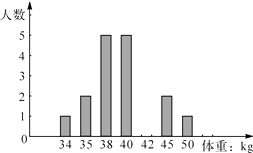
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心,顺次连接A、O1、B、O2 . 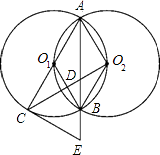
(1)求证:四边形AO1BO2是菱形;
(2)过直径AC的端点C作⊙O1的切线CE交AB的延长线于E,连接CO2交AE于D,求证:CE=2O2D;
(3)在(2)的条件下,若△AO2D的面积为1,求△BO2D的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:
①△BDF≌△DCE;②∠BMD=120°;③△AMH是等边三角形;④S四边形ABMD= ![]() AM2 .
AM2 .
其中正确结论的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)某地区为了鼓励市民节约用水,计划实行生活用水按阶梯式水价计费,每月用水量不超过10吨(含10吨)时,每吨按基础价收费;每月用水量超过10吨时,超过的部分每吨按调节价收费.例如,第一个月用水16吨,需交水费17.8元,第二个月用水20吨,需交水费23元.
(1)求每吨水的基础价和调节价;
(2)设每月用水量为n吨,应交水费为m元,写出m与n之间的函数解析式;
(3)若某月用水12吨,应交水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校有1500名学生参加首届“我爱我们的课堂”为主题的图片制作比赛,赛后随机抽取部分参赛学生的成绩进行整理并制作成图表如图:
分数段 | 频数 | 频率 |
60≤x<70 | 40 | 0.40 |
70≤x<80 | 35 | b |
80≤x<90 | a | 0.15 |
90≤x<100 | 10 | 0.10 |
频率分布统计表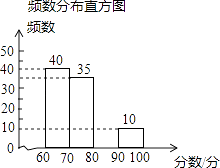
请根据上述信息,解答下列问题:
(1)分别求出a、b的值;
(2)请补全频数分布直方图;
(3)如果将比赛成绩80分以上(含80分)定为优秀,那么优秀率是多少?并且估算该校参赛学生获得优秀的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=30°,P是OA上的一点,OP=24cm,以r为半径作⊙P. 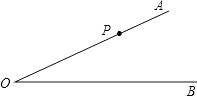
(1)若r=12cm,试判断⊙P与OB位置关系;
(2)若⊙P与OB相离,试求出r需满足的条件.
查看答案和解析>>
科目:初中数学 来源: 题型:
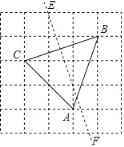
【题目】如图,方格中小正方形的边长为1,△ABC的三个顶点和线段EF的两个端点都在小正方形的格点(顶点)上,小明在观察探究时得到以下四个结论:
①△ABC是等边三角形;②△ABC的周长是![]() ;
;
③△ABC的面积是4;④直线EF是线段BC的垂直平分线.
你认为以上结论中,正确的序号有_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com