
| 板房型号 | 甲种板材 | 乙种板材 | 安置人数 |
| A型板房 | 54m2 | 26m2 | 5 |
| B型板房 | 78m2 | 41m2 | 8 |
分析 (1)设有x人生产甲种板材,那么就有(140-x)人生产乙种板材,根据每人每天能生产甲种板材30 m2或乙种板材20 m2,他们用相同的时间完成各自的生产任务,可列方程求解.
(2)设生产A种板房y间,B种板房(400-y)间,根据拥有的甲种板材24000 m2和乙种板材12000m2的材料,和搭建每种一间房所有的材料情况可列出不等式组,可见B越多容纳的人越多,从而得出答案.
解答 解:(1)设有x人生产甲种板材,
$\frac{24000}{30x}$=$\frac{12000}{20(140-x)}$,
解得:x=80,
经检验x=80是分式方程的解,
则乙种板材生产的人数是:140-80=60(人);
答:安排80人生产甲种板材,60人生产乙种板材.
(2)设生产A种板房y型,B种板房(400-y)型,
安置人数为5y+8(400-y)=-3y+3200,
$\left\{\begin{array}{l}{54y+78(400-y)≤24000}\\{26y+41(400-y)≤12000}\end{array}\right.$,
解得:y≥300,
因为-3<0,
所以当y=300时安置的人数最多,
300×5+(400-300)×8=2300(人).
故最多能安置2300人.
点评 本题考查了分式方程的应用,设出人数,根据时间做为等量关系列出方程求出解,第(2)问中以消耗的木材小于等于拥有的木材做为不等量关系列出不等式组求解,且B房越多,安置的人数越多,可得结果.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
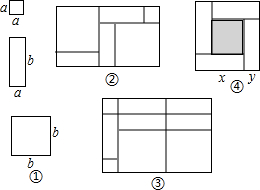 一天,王明和李玲玩纸片拼图游戏,发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式.比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2.
一天,王明和李玲玩纸片拼图游戏,发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式.比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 平均月用水量 | 不超过13.5立方米的部分 | 超过13.5立方米不超过23立方米的部分 | 超过23立方米的部分 |
| 收费标准(元/立方米) | 3.8 | 4.65 | 7.18 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com