
 如图:AB是半圆的直径,O是圆心,C、D是半圆上的两点,若AB=4,弦AC=CD=1.
如图:AB是半圆的直径,O是圆心,C、D是半圆上的两点,若AB=4,弦AC=CD=1. |
| AC |
 |
| CD |
 解:(1)∵AC=CD=1,
解:(1)∵AC=CD=1, |
| AC |
 |
| CD |
| ||
| 2 |
| AE |
| OA |
| ||||
| 2 |
| ||
| 4 |
| ||
| 2 |
| 15 |
| 15 |
| 7 |
| 2 |


科目:初中数学 来源: 题型:
| 国家 | 美国 | 日本 | 德国 | 法国 |
| 汽车产量 | 1200 | 1020 | 470 | 350 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
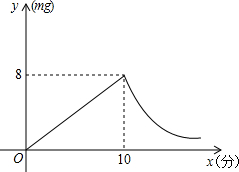 为预防感冒,小王家在家中燃烧艾草,已知艾草燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(分钟)成正比例;燃烧停止后,y与x成反比例(如图所示).据图象上信息解答下列问题:
为预防感冒,小王家在家中燃烧艾草,已知艾草燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(分钟)成正比例;燃烧停止后,y与x成反比例(如图所示).据图象上信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
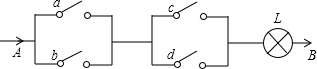 如图所示,有一电路AB是由如图所示的开关控制,闭合a,b,c,d四个开关中的任意两个开关.
如图所示,有一电路AB是由如图所示的开关控制,闭合a,b,c,d四个开关中的任意两个开关.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com