
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпy=ax2+bx+cЃЈaЃМ0ЃЉгыxжсНЛгкAЃЈЉ2ЃЌ0ЃЉЁЂBЃЈ4ЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкЕуCЃЌЧвOC=2OAЃЎ
ЃЈ1ЃЉЪдЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉжБЯпy=kx+1ЃЈkЃО0ЃЉгыyжсНЛгкЕуDЃЌгыХзЮяЯпНЛгкЕуPЃЌгыжБЯпBCНЛгкЕуMЃЌМЧm=![]() ЃЌЪдЧѓmЕФзюДѓжЕМАДЫЪБЕуPЕФзјБъЃЛ
ЃЌЪдЧѓmЕФзюДѓжЕМАДЫЪБЕуPЕФзјБъЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЕуQЪЧxжсЩЯЕФвЛИіЖЏЕуЃЌЕуNЪЧзјБъЦНУцФкЕФвЛЕуЃЌЪЧЗёДцдкетбљЕФЕуQЁЂNЃЌЪЙЕУвдPЁЂDЁЂQЁЂNЫФЕузщГЩЕФЫФБпаЮЪЧОиаЮЃПШчЙћДцдкЃЌЧыЧѓГіЕуNЕФзјБъЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉy=Љ![]() ЃЈx+2ЃЉЃЈxЉ4ЃЉЛђy=Љ
ЃЈx+2ЃЉЃЈxЉ4ЃЉЛђy=Љ![]() x2+x+4Лђy=Љ
x2+x+4Лђy=Љ![]() ЃЈxЉ1ЃЉ2+
ЃЈxЉ1ЃЉ2+![]() ЃЎЃЈ2ЃЉзюДѓжЕЮЊ
ЃЎЃЈ2ЃЉзюДѓжЕЮЊ![]() ЃЌДЫЪБPЃЈ2ЃЌ4ЃЉЃЎЃЈ3ЃЉЃЈ
ЃЌДЫЪБPЃЈ2ЃЌ4ЃЉЃЎЃЈ3ЃЉЃЈ![]() ЃЌ3ЃЉЛђЃЈ6ЃЌЉ3ЃЉЃЎ
ЃЌ3ЃЉЛђЃЈ6ЃЌЉ3ЃЉЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЩшХзЮяЯпЕФНтЮіЪНЮЊy=aЃЈx+2ЃЉЃЈxЉ4ЃЉЃЌИљОнвбжЊЬѕМўЧѓЕУЕуCЕФзјБъДњШыНтЮіЪНЧѓЕУaжЕЃЌМДПЩЕУХзЮяЯпЕФНтЮіЪНЃЛЃЈ2ЃЉзїPEЁЭxжсгкEЃЌНЛBCгкFЃЌвзжЄЁїCMDЁзЁїFMPЃЌИљОнЯрЫЦШ§НЧаЮЕФаджЪПЩЕУm=![]() ЃЌЩшPЃЈnЃЌЉ
ЃЌЩшPЃЈnЃЌЉ![]() n2+n+4ЃЉЃЌдђFЃЈnЃЌЉn+4ЃЉЃЌгУnБэЪОГіPFЕФГЄЃЌДгЖјЕУЕНmЁЂnЕФЖўДЮКЏЪ§ЙиЯЕЪНЃЌРћгУЖўДЮКЏЪ§ЕФаджЪНтОіЮЪЬтМДПЩЃЛЃЈ3ЃЉДцдкетбљЕФЕуQЁЂNЃЌЪЙЕУвдPЁЂDЁЂQЁЂNЫФЕузщГЩЕФЫФБпаЮЪЧОиаЮЃЌЗжDPЪЧОиаЮЕФБпКЭDPЪЧОиаЮЕФЖдНЧЯпСНжжЧщПіЧѓЕуNЕФзјБъ.
n2+n+4ЃЉЃЌдђFЃЈnЃЌЉn+4ЃЉЃЌгУnБэЪОГіPFЕФГЄЃЌДгЖјЕУЕНmЁЂnЕФЖўДЮКЏЪ§ЙиЯЕЪНЃЌРћгУЖўДЮКЏЪ§ЕФаджЪНтОіЮЪЬтМДПЩЃЛЃЈ3ЃЉДцдкетбљЕФЕуQЁЂNЃЌЪЙЕУвдPЁЂDЁЂQЁЂNЫФЕузщГЩЕФЫФБпаЮЪЧОиаЮЃЌЗжDPЪЧОиаЮЕФБпКЭDPЪЧОиаЮЕФЖдНЧЯпСНжжЧщПіЧѓЕуNЕФзјБъ.
ЪдЬтНтЮіЃК
ЃЈ1ЃЉвђЮЊХзЮяЯпy=ax2+bx+cОЙ§AЃЈЉ2ЃЌ0ЃЉЁЂBЃЈ4ЃЌ0ЃЉСНЕуЃЌЩшy=aЃЈx+2ЃЉЃЈxЉ4ЃЉЃЌ
ЁпOC=2OAЃЌOA=2ЃЌ
ЁрCЃЈ0ЃЌ4ЃЉЃЌДњШыХзЮяЯпЕФНтЮіЪНЕУЕНa=Љ![]() ЃЌ
ЃЌ
Ёрy=Љ![]() ЃЈx+2ЃЉЃЈxЉ4ЃЉЛђy=Љ
ЃЈx+2ЃЉЃЈxЉ4ЃЉЛђy=Љ![]() x2+x+4Лђy=Љ
x2+x+4Лђy=Љ![]() ЃЈxЉ1ЃЉ2+
ЃЈxЉ1ЃЉ2+![]() ЃЎ
ЃЎ
ЃЈ2ЃЉШчЭМ1жаЃЌзїPEЁЭxжсгкEЃЌНЛBCгкFЃЎ
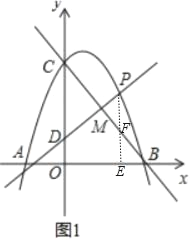
ЁпCDЁЮPEЃЌ
ЁрЁїCMDЁзЁїFMPЃЌ
Ёрm=![]() =
=![]() ЃЌ
ЃЌ
ЁпжБЯпy=kx+1ЃЈkЃО0ЃЉгыyжсНЛгкЕуDЃЌдђDЃЈ0ЃЌ1ЃЉЃЌ
ЁпBCЕФНтЮіЪНЮЊy=Љx+4ЃЌ
ЩшPЃЈnЃЌЉ![]() n2+n+4ЃЉЃЌдђFЃЈnЃЌЉn+4ЃЉЃЌ
n2+n+4ЃЉЃЌдђFЃЈnЃЌЉn+4ЃЉЃЌ
ЁрPF=Љ![]() n2+n+4ЉЃЈЉn+4ЃЉ=Љ
n2+n+4ЉЃЈЉn+4ЃЉ=Љ![]() ЃЈnЉ2ЃЉ2+2ЃЌ
ЃЈnЉ2ЃЉ2+2ЃЌ
Ёрm=![]() =Љ
=Љ![]() ЃЈnЉ2ЃЉ2+
ЃЈnЉ2ЃЉ2+![]() ЃЌ
ЃЌ
ЁпЉ![]() ЃМ0ЃЌ
ЃМ0ЃЌ
ЁрЕБn=2ЪБЃЌmгазюДѓжЕЃЌзюДѓжЕЮЊ![]() ЃЌДЫЪБPЃЈ2ЃЌ4ЃЉЃЎ
ЃЌДЫЪБPЃЈ2ЃЌ4ЃЉЃЎ
ЃЈ3ЃЉДцдкетбљЕФЕуQЁЂNЃЌЪЙЕУвдPЁЂDЁЂQЁЂNЫФЕузщГЩЕФЫФБпаЮЪЧОиаЮЃЎ
ЂйЕБDPЪЧОиаЮЕФБпЪБЃЌгаСНжжЧщаЮЃЌ
aЁЂШчЭМ2Љ1жаЃЌЫФБпаЮDQNPЪЧОиаЮЪБЃЌ
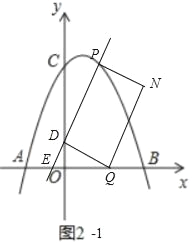
гаЃЈ2ЃЉПЩжЊPЃЈ2ЃЌ4ЃЉЃЌДњШыy=kx+1жаЃЌЕУЕНk=![]() ЃЌ
ЃЌ
ЁржБЯпDPЕФНтЮіЪНЮЊy=![]() x+1ЃЌПЩЕУDЃЈ0ЃЌ1ЃЉЃЌEЃЈЉ
x+1ЃЌПЩЕУDЃЈ0ЃЌ1ЃЉЃЌEЃЈЉ![]() ЃЌ0ЃЉЃЌ
ЃЌ0ЃЉЃЌ
гЩЁїDOEЁзЁїQODПЩЕУ![]() =
=![]() ЃЌ
ЃЌ
ЁрOD2=OEOQЃЌ
Ёр1=![]() OQЃЌ
OQЃЌ
ЁрOQ=![]() ЃЌ
ЃЌ
ЁрQЃЈ![]() ЃЌ0ЃЉЃЎ
ЃЌ0ЃЉЃЎ
ИљОнОиаЮЕФаджЪЃЌНЋЕуPЯђгвЦНвЦ![]() ИіЕЅЮЛЃЌЯђЯТЦНвЦ1ИіЕЅЮЛЕУЕНЕуNЃЌ
ИіЕЅЮЛЃЌЯђЯТЦНвЦ1ИіЕЅЮЛЕУЕНЕуNЃЌ
ЁрNЃЈ2+![]() ЃЌ4Љ1ЃЉЃЌМДNЃЈ
ЃЌ4Љ1ЃЉЃЌМДNЃЈ![]() ЃЌ3ЃЉ
ЃЌ3ЃЉ
bЁЂШчЭМ22жаЃЌЫФБпаЮPDNQЪЧОиаЮЪБЃЌ
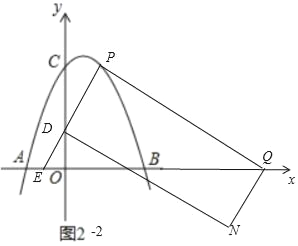
ЁпжБЯпPDЕФНтЮіЪНЮЊy=![]() x+1ЃЌPQЁЭPDЃЌ
x+1ЃЌPQЁЭPDЃЌ
ЁржБЯпPQЕФНтЮіЪНЮЊy=Љ![]() x+
x+![]() ЃЌ
ЃЌ
ЁрQЃЈ8ЃЌ0ЃЉЃЌ
ИљОнОиаЮЕФаджЪПЩжЊЃЌНЋЕуDЯђгвЦНвЦ6ИіЕЅЮЛЃЌЯђЯТЦНвЦ4ИіЕЅЮЛЕУЕНЕуNЃЌ
ЁрNЃЈ0+6ЃЌ1Љ4ЃЉЃЌМДNЃЈ6ЃЌЉ3ЃЉЃЎ
ЂкЕБDPЪЧЖдНЧЯпЪБЃЌЩшQЃЈxЃЌ0ЃЉЃЌдђQD2=x2+1ЃЌQP2=ЃЈxЉ2ЃЉ2+42ЃЌPD2=13ЃЌ
ЁпQЪЧжБНЧЖЅЕуЃЌ
ЁрQD2+QP2=PD2ЃЌ
Ёрx2+1+ЃЈxЉ2ЃЉ2+16=13ЃЌ
ећРэЕУx2Љ2x+4=0ЃЌЗНГЬЮоНтЃЌДЫжжЧщаЮВЛДцдкЃЌ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФЕуNзјБъЮЊЃЈ![]() ЃЌ3ЃЉЛђЃЈ6ЃЌЉ3ЃЉЃЎ
ЃЌ3ЃЉЛђЃЈ6ЃЌЉ3ЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭМЂйЪЧаЁУїдкНЁЩэЦїВФЩЯНјаабіЮдЦ№зјЖЭСЖЪБЕФЧщОАЃЌЭМЂкЪЧаЁУїЖЭСЖЪБЩЯАыЩэгЩONЮЛжУдЫЖЏЕНгыЕиУцДЙжБЕФOMЮЛжУЪБЕФЪОвтЭМЃЎвбжЊAC=0.66УзЃЌBD=0.26УзЃЌІС=20ЁуЃЎЃЈВЮПМЪ§ОнЃКsin20ЁуЁж0.342ЃЌcos20ЁуЁж0.940ЃЌtan20ЁуЁж0.364ЃЉ

ЃЈ1ЃЉЧѓABЕФГЄЃЈОЋШЗЕН0.01УзЃЉЃЛ
ЃЈ2ЃЉШєВтЕУON=0.8УзЃЌЪдМЦЫуаЁУїЭЗЖЅгЩNЕудЫЖЏЕНMЕуЕФТЗОЖ![]() ЕФГЄЖШЃЎЃЈНсЙћБЃСєІаЃЉ
ЕФГЄЖШЃЎЃЈНсЙћБЃСєІаЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуA,BдкЪ§жсЩЯБэЪОЕФЪ§ЗжБ№ЮЊ-4КЭ+16ЃЌA,BСНЕуМфЕФОрРыПЩМЧЮЊAB
![]()
(1) ЕуCдкЪ§жсЩЯA,BСНЕужЎМфЃЌЧвAC=BC,дђCЕуЖдгІЕФЪ§ЪЧ_________
(2) ЕуCдкЪ§жсЩЯA,BСНЕужЎМфЃЌЧвBC=4AC,дђCЕуЖдгІЕФЪ§ЪЧ_________
(3) ЕуCдкЪ§жсЩЯ,ЧвAC+BC=30ЃЌЧѓЕуCЖдгІЕФЪ§?
(4) ШєЕуAдкЪ§жсЩЯБэЪОЕФЪ§ЪЧa,BБэЪОЕФЪ§ЪЧb,дђAB=_________
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуPЪЧБпГЄЮЊ![]() ЕФе§ЗНаЮABCDЕФЖдНЧЯпBDЩЯЕФЖЏЕуЃЌЙ§ЕуPЗжБ№зїPEЁЭBCгкЕуEЃЌPFЁЭDCгкЕуFЃЌСЌНгAPВЂбгГЄЃЌНЛЩфЯпBCгкЕуHЃЌНЛЩфЯпDCгкЕуMЃЌСЌНгEFНЛAHгкЕуGЃЌЕБЕуPдкBDЩЯдЫЖЏЪБЃЈВЛАќРЈBЁЂDСНЕуЃЉЃЌвдЯТНсТлжаЃКЂйMF=MCЃЛЂкAHЁЭEFЃЛЂлAP2=PMPHЃЛЂмEFЕФзюаЁжЕЪЧ
ЕФе§ЗНаЮABCDЕФЖдНЧЯпBDЩЯЕФЖЏЕуЃЌЙ§ЕуPЗжБ№зїPEЁЭBCгкЕуEЃЌPFЁЭDCгкЕуFЃЌСЌНгAPВЂбгГЄЃЌНЛЩфЯпBCгкЕуHЃЌНЛЩфЯпDCгкЕуMЃЌСЌНгEFНЛAHгкЕуGЃЌЕБЕуPдкBDЩЯдЫЖЏЪБЃЈВЛАќРЈBЁЂDСНЕуЃЉЃЌвдЯТНсТлжаЃКЂйMF=MCЃЛЂкAHЁЭEFЃЛЂлAP2=PMPHЃЛЂмEFЕФзюаЁжЕЪЧ![]() ЃЎЦфжае§ШЗНсТлЪЧЃЈЁЁЁЁЃЉ
ЃЎЦфжае§ШЗНсТлЪЧЃЈЁЁЁЁЃЉ

A. ЂйЂл B. ЂкЂл C. ЂкЂлЂм D. ЂкЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГМьаоаЁзщДг![]() ЕиГіЗЂЃЌдкЖЋЮїЯђЕФТэТЗЩЯМьаоЯпТЗЃЌШчЙћЙцЖЈЯђЖЋааЪЛЮЊе§ЃЌЯђЮїааЪЛЮЊИКЃЌвЛЬьжаЦпДЮааЪЛМЭТМШчЯТЃЎЃЈЕЅЮЛЃК
ЕиГіЗЂЃЌдкЖЋЮїЯђЕФТэТЗЩЯМьаоЯпТЗЃЌШчЙћЙцЖЈЯђЖЋааЪЛЮЊе§ЃЌЯђЮїааЪЛЮЊИКЃЌвЛЬьжаЦпДЮааЪЛМЭТМШчЯТЃЎЃЈЕЅЮЛЃК![]() ЃЉ
ЃЉ
ЕквЛДЮ | ЕкЖўДЮ | ЕкШ§ДЮ | ЕкЫФДЮ | ЕкЮхДЮ | ЕкСљДЮ | ЕкЦпДЮ |
|
|
|
|
|
|
|
![]() ЧѓЪеЙЄЪБЃЌМьаоаЁзщдк
ЧѓЪеЙЄЪБЃЌМьаоаЁзщдк![]() ЕиЕФФФИіЗНЯђЃПОрРы
ЕиЕФФФИіЗНЯђЃПОрРы![]() ЕиЖрдЖЃП
ЕиЖрдЖЃП
![]() дкЕкМИДЮМЭТМЪБОр
дкЕкМИДЮМЭТМЪБОр![]() ЕизюдЖЃП
ЕизюдЖЃП
![]() ШєЦћГЕааЪЛУПЧЇУзКФгЭ
ШєЦћГЕааЪЛУПЧЇУзКФгЭ![]() Щ§ЃЌЮЪДг
Щ§ЃЌЮЪДг![]() ЕиГіЗЂЃЌМьаоНсЪјКѓдйЛиЕН
ЕиГіЗЂЃЌМьаоНсЪјКѓдйЛиЕН![]() ЕиЙВКФгЭЖрЩйЩ§ЃП
ЕиЙВКФгЭЖрЩйЩ§ЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮТжнЯэгаЁАжаЙњБЪЖМЁБжЎГЦЃЌЦфВњЦЗГЉЯњШЋЧђЃЌФГжЦБЪЦѓвЕгћНЋnМўВњЦЗдЫЭљAЃЌBЃЌCШ§ЕиЯњЪлЃЌвЊЧѓдЫЭљCЕиЕФМўЪ§ЪЧдЫЭљAЕиМўЪ§ЕФ2БЖЃЌИїЕиЕФдЫЗбШчЭМЫљЪОЃЎЩшАВХХxМўВњЦЗдЫЭљAЕиЃЎ
ЃЈ1ЃЉЕБn=200ЪБЃЌЂйИљОнаХЯЂЬюБэЃК
AЕи | BЕи | CЕи | КЯМЦ | |
ВњЦЗМўЪ§ЃЈМўЃЉ | x | 2x | 200 | |
дЫЗбЃЈдЊЃЉ | 30x |
ЂкШєдЫЭљBЕиЕФМўЪ§ВЛЖргкдЫЭљCЕиЕФМўЪ§ЃЌзмдЫЗбВЛГЌЙ§4000дЊЃЌдђгаФФМИжждЫЪфЗНАИЃП
ЃЈ2ЃЉШєзмдЫЗбЮЊ5800дЊЃЌЧѓnЕФзюаЁжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпyЃНkxЃ1гыxжсЁЂyжсЗжБ№НЛгкBЁЂCСНЕуЃЌOBЃКOCЃН![]() .
.
(1)ЧѓBЕуЕФзјБъКЭkЕФжЕЃЎ
(2)ШєЕуA(xЃЌy)ЪЧЕквЛЯѓЯоФкЕФжБЯпyЃНkxЃ1ЩЯЕФвЛИіЖЏЕуЃЌЕБЕуAдЫЖЏЙ§ГЬжаЃЌЪдаДГіЁїAOBЕФУцЛ§SгыxЕФКЏЪ§ЙиЯЕЪНЃЛ
(3)дкЃЈ2ЃЉЕФЬѕМўЯТЃЌЕБЕуAдЫЖЏЕНЪВУДЮЛжУЪБЃЌЁїAOBЕФУцЛ§ЪЧ![]() .
.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСВФСЯ:
ШчЙћвЛИіШ§НЧаЮЕФШ§БпГЄЗжБ№ЮЊaЃЌbЃЌcЃЌМЧp=![]() ЃЌФЧУДетИіШ§НЧаЮЕФУцЛ§S=
ЃЌФЧУДетИіШ§НЧаЮЕФУцЛ§S=![]() .етИіЙЋЪННаЁАКЃТзЙЋЪНЁБЃЌЫќЪЧРћгУШ§НЧаЮШ§ЬѕБпЕФБпГЄжБНгЧѓШ§НЧаЮУцЛ§ЕФЙЋЪНЁЃжаЙњЕФЧиОХЩивВЕУГіСЫРрЫЦЕФЙЋЪНЃЌГЦШ§аБЧѓЛ§ЪѕЃЌЙЪетИіЙЋЪНгжБЛГЦЮЊЁАКЃТзЧи---ОХЩиЙЋЪНЁБЭъГЩЯТСаЮЪЬт:
.етИіЙЋЪННаЁАКЃТзЙЋЪНЁБЃЌЫќЪЧРћгУШ§НЧаЮШ§ЬѕБпЕФБпГЄжБНгЧѓШ§НЧаЮУцЛ§ЕФЙЋЪНЁЃжаЙњЕФЧиОХЩивВЕУГіСЫРрЫЦЕФЙЋЪНЃЌГЦШ§аБЧѓЛ§ЪѕЃЌЙЪетИіЙЋЪНгжБЛГЦЮЊЁАКЃТзЧи---ОХЩиЙЋЪНЁБЭъГЩЯТСаЮЪЬт:
ШчЭМЃЌдкЁїABCжаЃЌa=7ЃЌb=5ЃЌc=6.
ЃЈ1ЃЉЧѓЁїABCЕФУцЛ§;
ЃЈ2ЃЉЩшABБпЩЯЕФИпЮЊh1ЃЌACБпЩЯЕФИпЮЊh2ЃЌЧѓh1 +h2ЕФжЕ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкФГвЛГЧЪаУРЛЏЙЄГЬеаБъЪБЃЌгаМзЁЂввСНИіЙЄГЬЖгЭЖБъЃЎОВтЫуЃКМзЖгЕЅЖРЭъГЩетЯюЙЄГЬашвЊ60ЬьЃЌввЖгЕЅЖРЭъГЩетЯюЙЄГЬашвЊ90ЬьЃЛШєгЩМзЖгЯШзі20ЬьЃЌЪЃЯТЕФЙЄГЬгЩМзЁЂввСНЖгКЯзіЭъГЩЃЎ
ЃЈ1ЃЉМзЁЂввСНЖгКЯзїЖрЩйЬьЃП
ЃЈ2ЃЉМзЖгЪЉЙЄвЛЬьашИЖЙЄГЬПю3.5ЭђдЊЃЌввЖгЪЉЙЄвЛЬьашИЖЙЄГЬПю2ЭђдЊЃЎШєИУЙЄГЬМЦЛЎдк70ЬьФкЭъГЩЃЌдкВЛГЌЙ§МЦЛЎЬьЪ§ЕФЧАЬсЯТЃЌЪЧгЩМзЖгЛђввЖгЕЅЖРЭъГЩИУЙЄГЬЪЁЧЎЃПЛЙЪЧгЩМзввСНЖгШЋГЬКЯзїЭъГЩИУЙЄГЬЪЁЧЎЃП
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com