练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    （本小题满分7分）
    向阳花卉基地出售两种花卉——百合和玫瑰，其单价为：玫瑰4元/株，百合5元/株，如果同一客户所购的玫瑰数量大于1200株，那么每株玫瑰还可降价1元。现某鲜花店向向阳花卉基地采购玫瑰1000株～1500株，百合若干株，此鲜花店本次用于采购玫瑰和百合恰好花去了9000元。然后再以玫瑰5元、百合6.5元的价格卖出。问：此鲜花店应如何采购这两种鲜花才能使获得的毛利润最大？
    （注：1000株～1500株，表示大于或等于1000株，且小于或等于1500株。
    毛利润＝鲜花店卖出百合和玫瑰所获的总金额—购进百合和玫瑰的所需的总金额

    采购百合900株，采购玫瑰1500株，毛利润最大为4350元

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （本小题满分12分）

    如图，在直角梯形ABCD中，AD∥BC，，AD = 6，BC = 8，，点M是BC的中点．点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动，到达点B后立刻以原速度沿BM返回；点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动．在点P，Q的运动过程中，以PQ为边作等边三角形EPQ，使它与梯形ABCD在射线BC的同侧．点P，Q同时出发，当点P返回到点M时停止运动，点Q也随之停止．设点P，Q运动的时间是t秒(t＞0)．

     

     

     

     

     

     

     


    1.（1）设PQ的长为y，在点P从点M向点B运动的过程中，写出y与t之间的函数关系式（不必写t的取值范围）．

    2.（2）当BP = 1时，求△EPQ与梯形ABCD重叠部分的面积．

    3.（3）随着时间t的变化，线段AD会有一部分被△EPQ覆盖，被覆盖线段的长度在某个时刻会达到最大值，请回答：该最大值能否持续一个时段？若能，直接写出t的取值范围；若不能，请说明理由．

     

    查看答案和解析>>

    科目：初中数学 来源：2010年高级中等学校招生全国统一考试数学卷（云南昆明） 题型：解答题

    （本小题满分11分）

    二次函数的图像如图8所示，请将此图像向右平移1个单位，再向下平移2个单位.

    （1）画出经过两次平移后所得到的图像，并写出函数的解析式.

    （2）求经过两次平移后的图像与x轴的交点坐标，当x满足什么条件时，函数值大于0？

     

    查看答案和解析>>

    科目：初中数学 来源：2010年海南省海口市初三第一学期期中数学卷 题型：解答题

    （本小题满分12分）

    如图16，在直角梯形ABCD中，AD∥BC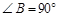，，AD = 6，BC = 8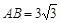，，点M是BC的中点．点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动，到达点B后立刻以原速度沿BM返回；点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动．在点P，Q的运动过程中，以PQ为边作等边三角形EPQ，使它与梯形ABCD在射线BC的同侧．点P，Q同时出发，当点P返回到点M时停止运动，点Q也随之停止．

    设点P，Q运动的时间是t秒(t＞0)．

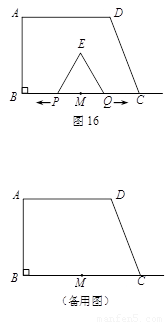
    （1）设PQ的长为y，在点P从点M向点B运动的过程中，写出y与t之间的函数关系式（不必写t的取值范围）．

    （2）当BP = 1时，求△EPQ与梯形ABCD重叠部分的面积．

    （3）随着时间t的变化，线段AD会有一部分被△EPQ覆盖，被覆盖线段的长度在某个时刻会达到最大值，请回答：该最大值能否持续一个时段？若能，直接写出t的取值范围；若不能，请说明理由．

     

    查看答案和解析>>

    科目：初中数学 来源：2010-2011年江苏省九年级第二学期模拟考试数学卷 题型：解答题

    （本小题满分12分）已知直角坐标系中菱形ABCD的位置如图，C，D两点的坐标分别为(4,0)，(0,3).现有两动点P,Q分别从A,C同时出发，点P沿线段AD向终点D运动，点Q沿折线CBA向终点A运动，设运动时间为t秒.

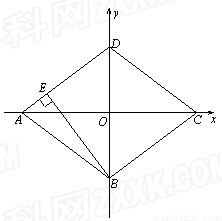
    1.(1)填空：菱形ABCD的边长是  ▲  、面积是

      ▲  、 高BE的长是  ▲  ；

    2.(2)探究下列问题：

    ①若点P的速度为每秒1个单位，点Q的速度为每秒2个单位.当点Q在线段BA上时，求△APQ的面积S关于t的函数关系式，以及S的最大值；

    ②若点P的速度为每秒1个单位，点Q的速度变为每秒k个单位，在运动过程中,任何时刻都有相应的k值，使得△APQ沿它的一边翻折，翻折前后两个三角形组成的四边形为菱形.请探究当t = 4 秒时的情形，并求出k的值.

     

    查看答案和解析>>

    科目：初中数学 来源：2010-2011年江苏省九年级第二学期模拟考试数学卷 题型：解答题

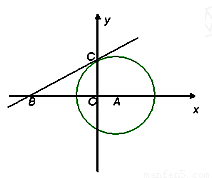
    （本小题满分10分）已知：如图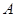，⊙与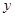轴交于C、D两点，圆心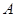的坐标

    为（1，0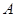），⊙的半径为，过点C作⊙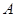的切线交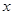轴于点B（－4，0）

     

     

     

     

     

     

     

     

     


    1.（1）求切线BC的解析式；

    2.（2）若点P是第一象限内⊙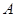上一点，过点P作⊙A的切线与直线BC相交于点G，

    且∠CGP＝120°，求点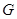的坐标；

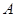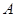    3.（3）向左移动⊙（圆心始终保持在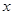轴上），与直线BC交于E、F，在移动过程中是否存在点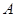，使得△AEF是直角三角形？若存在，求出点 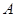的坐标，若不存在，请说明理由．

     

    查看答案和解析>>

    同步练习册答案