

分析 (1)设交点式为y=a(x+1)(x-3),然后把C点坐标代入求出a即可得到抛物线解析式;
(2)①作DE⊥x轴于E,如图1,先证明△AOT∽△AED,利用相似比得到AE=5,OT=$\frac{1}{5}$DE,则OE=4,即D点的横坐标为4,利用抛物线解析式可得到D(4,$\frac{5}{2}$),则DE=$\frac{5}{2}$,于是可计算出OT=$\frac{1}{5}$DE=$\frac{1}{2}$,从而得到T点坐标;
②过点P作PF∥AT交y轴于F,如图2,当直线PF与抛物线只有一个公共点P时,点P到直线AT的距离最大,根据三角形面积公式可判定此时△ATP的面积的最大,S△APT=$\frac{9}{4}$,设T(0,t),利用S△AFT=S△APT=$\frac{9}{4}$可得到OF=TF-OT=$\frac{9}{2}$-t,则F(0,t-$\frac{9}{2}$),再表示出直线AT的解析式为y=tx+t,利用两直线平行的问题可设直线PF的解析式为y=tx+t-$\frac{9}{2}$,根据抛物线与直线的交点问题列方程组$\left\{\begin{array}{l}{y=\frac{1}{2}{x}^{2}-x-\frac{3}{2}}\\{y=tx+t-\frac{9}{2}}\end{array}\right.$,消去y得到$\frac{1}{2}$x2-(t+1)x+3-t=0,再根据判别式的意义得到关于t的方程,最后解关于t的方程即可.
解答 解:(1)设抛物线解析式为y=a(x+1)(x-3),
把C(0,-$\frac{3}{2}$)代入得a•1•(-3)=-$\frac{3}{2}$,解得a=$\frac{1}{2}$,
所以抛物线解析式为y=$\frac{1}{2}$(x+1)(x-3),即y=$\frac{1}{2}$x2-x-$\frac{3}{2}$;
(2)①作DE⊥x轴于E,如图1, ∵DE∥OT,
∵DE∥OT,
∴△AOT∽△AED,
∴$\frac{AO}{AE}$=$\frac{OT}{DE}$=$\frac{AT}{AD}$,即$\frac{1}{AE}$=$\frac{OT}{DE}$=$\frac{1}{5}$,解得AE=5,OT=$\frac{1}{5}$DE,
∴OE=4,
当x=4时,y=$\frac{1}{2}$x2-x-$\frac{3}{2}$=$\frac{1}{2}$×16-4-$\frac{3}{2}$=$\frac{5}{2}$,
∴D(4,$\frac{5}{2}$),
∴DE=$\frac{5}{2}$,
∴OT=$\frac{1}{5}$DE=$\frac{1}{2}$,
∴T(0,$\frac{1}{2}$);
②过点P作PF∥AT交y轴于F,如图2,
当直线PF与抛物线只有一个公共点P时,点P到直线AT的距离最大,此时△ATP的面积的最大,S△APT=$\frac{9}{4}$,
设T(0,t),
∵PF∥AT,
∴S△AFT=S△APT=$\frac{9}{4}$,
∴$\frac{1}{2}$•1•TF=$\frac{9}{4}$,解得TF=$\frac{9}{2}$,
∴OF=TF-OT=$\frac{9}{2}$-t,
∴F(0,t-$\frac{9}{2}$),
设直线AT的解析式为y=kx+t,把A(-1,0)代入得-k+t=0,解得k=t,
∴直线AT的解析式为y=tx+t,
∵直线PF与直线AT平行,
∴直线PF的解析式为y=tx+t-$\frac{9}{2}$,
列方程组$\left\{\begin{array}{l}{y=\frac{1}{2}{x}^{2}-x-\frac{3}{2}}\\{y=tx+t-\frac{9}{2}}\end{array}\right.$,消去y得到$\frac{1}{2}$x2-(t+1)x+3-t=0,
△=(t+1)2-4•$\frac{1}{2}$•(3-t)=0,
整理得t2+4t-5=0,
解得t1=1,t2=-5(舍去),
∴T点坐标为(0,1).
点评 本题考查了二次函数的综合题:熟练掌握二次函数的图象上点的坐标特征和根的判别式的意义;会利用待定系数法法函数解析式,会求抛物线与一次函数图象的交点坐标;能构建相似三角形,利用相似比表示线段之间的关系.


科目:初中数学 来源: 题型:解答题
 二七纪念塔是我省郑州市的标志性建筑,某兴趣小组为了测量二七纪念塔的高度,进行了如下的研究.如图,AB为二七纪念塔,从地面C点看塔顶A点,仰角为45°,到建筑DE顶端E点后,从E点看塔顶A点,仰角为60°,C、D、B三点在同一直线上.已知建筑DE高度为35.3米,∠ECD=37°,求二七纪念塔AB的高度.(结果保留整数,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75;$\sqrt{3}$≈1.732)
二七纪念塔是我省郑州市的标志性建筑,某兴趣小组为了测量二七纪念塔的高度,进行了如下的研究.如图,AB为二七纪念塔,从地面C点看塔顶A点,仰角为45°,到建筑DE顶端E点后,从E点看塔顶A点,仰角为60°,C、D、B三点在同一直线上.已知建筑DE高度为35.3米,∠ECD=37°,求二七纪念塔AB的高度.(结果保留整数,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75;$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
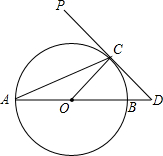 如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD.
如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在矩形ABCD中,E为AD的中点,连接BE、BD,过点A作AF⊥BE交BE于点F,连接FD.
已知:如图,在矩形ABCD中,E为AD的中点,连接BE、BD,过点A作AF⊥BE交BE于点F,连接FD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 气温℃ | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 天数/天 | 2 | 3 | x | 5 | 4 | y | z | 3 | 2 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com