Question

8．如图，在平面直角坐标系中，已知点A（2，3）、B（6，3），连接AB．如果对于平面内一点P，线段AB上都存在点Q，使得PQ≤1，那么称点P是线段AB的“附近点”．
（1）请判断点D（4.5，2.5）是否是线段AB的“附近点”；
（2）如果点H （m，n）在一次函数$y=\frac{6}{5}x-2$的图象上，且是线段AB的“附近点”，求m的取值范围；
（3）如果一次函数y=x+b的图象上至少存在一个“附近点”，请直接写出b的取值范围．

Answer 1

分析 （1）点P是线段AB的“附近点”的定义即可判断．
（2）首先求出直线$y=\frac{6}{5}x-2$与线段AB交于$（{\frac{25}{6}，3}）$，分①当$m≥\frac{25}{6}$时，②当$m≤\frac{25}{6}$时，列出不等式即可解决问题．
（3）如图，在RT△AMN中，AM=1，∠MAN=45°，则点M坐标（2-$\frac{\sqrt{2}}{2}$，3+$\frac{\sqrt{2}}{2}$），在RT△BEF中，BE=1，∠EBF=45°，则点E坐标（6+$\frac{\sqrt{2}}{2}$，3-$\frac{\sqrt{2}}{2}$）
分别求出直线经过点M、点E时的b的值，即可解决问题．

解答 解：（1）∵点D到线段AB的距离是0.5，
∴0.5＜1，
∴点D（4.5，2.5）是否是线段AB的“附近点”； 

（2）∵点H（m，n）是线段AB的“附近点”，点H（m，n）在直线$y=\frac{6}{5}x-2$上，
∴$n=\frac{6}{5}m-2$；
直线$y=\frac{6}{5}x-2$与线段AB交于$（{\frac{25}{6}，3}）$．
①当$m≥\frac{25}{6}$时，有$n=\frac{6}{5}m-2$≥3，
又AB∥x轴，∴此时点H（m，n）到线段AB的距离是n-3，
∴0≤n-3≤1，∴$\frac{25}{6}≤m≤5$．
②当$m≤\frac{25}{6}$时，有$n=\frac{6}{5}m-2$≤3，
又AB∥x轴，∴此时点H（m，n）到线段AB的距离是3-n，
∴0≤3-n≤1，∴$\frac{10}{3}≤m≤\frac{25}{6}$，
综上所述，$\frac{10}{3}≤m≤5$．

（3）如图，在RT△AMN中，AM=1，∠MAN=45°，则点M坐标（2-$\frac{\sqrt{2}}{2}$，3+$\frac{\sqrt{2}}{2}$），
在RT△BEF中，BE=1，∠EBF=45°，则点E坐标（6+$\frac{\sqrt{2}}{2}$，3-$\frac{\sqrt{2}}{2}$）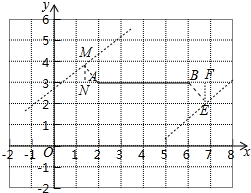

当直线y=x+b经过点M时，b=1+$\sqrt{2}$，
当直线y=x+b经过点E时，b=-3-$\sqrt{2}$，
∴-3-$\sqrt{2}$≤b≤1+$\sqrt{2}$．

点评 本题考查一次函数综合题、线段AB的“附近点”的定义等知识，解题的关键是连接题意，学会分类讨论，学会利用特殊点解决问题，属于中考压轴题．