
【题目】周末,小明和爸爸在400米的环形跑道上骑车锻炼,他们在同一地点沿着同一方向同时出发,骑行结束后两人有如下对话:

(1)他们的对话内容,求小明和爸爸的骑行速度,
(2)一次追上小明后,在第二次相遇前,再经过多少分钟,小明和爸爸相距50m?
【答案】(1)小明骑行速度为200m/分钟,爸爸骑行速度为400m/分钟;(2)爸爸第一次追上小明后,在第二次相遇前,再经过![]() 分或
分或![]() 钟,小明和爸爸相距50m.
钟,小明和爸爸相距50m.
【解析】
(1)设小明的骑行速度为x米/分钟,则爸爸的骑行速度为2x米/分钟,根据距离=速度差×时间即可得出关于x的一元一次方程,解之即可得出结论;
(2)设爸爸第一次追上小明后,在第二次相遇前,再经过y分钟,小明和爸爸跑道上相距50m.分第一次相遇后爸爸比小明多骑50米和350米两种情况考虑,根据距离=速度差×时间即可得出关于y的一元一次方程,解之即可得出结论.
(1)设小明的骑行速度为x米/分钟,则爸爸的骑行速度为2x米/分钟,
根据题意得:2(2x-x)=400,
解得:x=200,
∴2x=400.
答:小明的骑行速度为200米/分钟,爸爸的骑行速度为400米/分钟.
(2)设爸爸第一次追上小明后,在第二次相遇前,再经过y分钟,小明和爸爸跑道上相距50m,
①爸爸第一次追上小明后,在第二次相遇前,爸爸又比小明多骑了50米,
根据题意得:400y-200y=50,
解得:y=![]() ;
;
②爸爸第一次追上小明后,在第二次相遇前,爸爸又比小明多骑了350米,
根据题意得:400y-200y=350,
解得:y=![]() .
.
答:第二次相遇前,再经过![]() 或
或![]() 分钟,小明和爸爸跑道上相距50m.
分钟,小明和爸爸跑道上相距50m.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
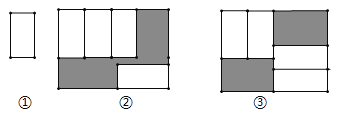
【题目】把四张大小相同的长方形卡片(如图①)按图②、图③两种放法放在一个底面为长方形(长为![]() ,宽为
,宽为![]() )的盒底上,底面未被卡片覆盖的部分用阴影表示,若记图②中阴影部分的周长为
)的盒底上,底面未被卡片覆盖的部分用阴影表示,若记图②中阴影部分的周长为![]() ,图③中阴影部分的周长为
,图③中阴影部分的周长为![]() ,则
,则![]() ___________.
___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费5元;方式二:不购买会员证,每次游泳付费9元.
设小明计划今年夏季游泳次数为x(x为正整数).
(I)根据题意,填写下表:
游泳次数 | 10 | 15 | 20 | … | x |
方式一的总费用(元) | 150 | 175 | ______ | … | ______ |
方式二的总费用(元) | 90 | 135 | ______ | … | ______ |
(Ⅱ)若小明计划今年夏季游泳的总费用为270元,选择哪种付费方式,他游泳的次数比较多?
(Ⅲ)当x>20时,小明选择哪种付费方式更合算?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,△
中,△![]() 的顶点
的顶点![]() 、
、![]() 在坐标轴上,点
在坐标轴上,点![]() 的坐标是(2,2).将△ABC沿
的坐标是(2,2).将△ABC沿![]() 轴向左平移得到△A1B1C1,点
轴向左平移得到△A1B1C1,点![]() 落在函数y=-
落在函数y=-![]() .如果此时四边形
.如果此时四边形![]() 的面积等于
的面积等于![]() ,那么点
,那么点![]() 的坐标是________.
的坐标是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
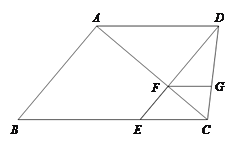
【题目】已知:如图,梯形ABCD中,AD∥BC,DE∥AB,![]() 与对角线
与对角线![]() 交于点
交于点![]() ,
,![]() ∥
∥![]() ,且FG=EF.
,且FG=EF.
(1)求证:四边形![]() 是菱形;
是菱形;
(2)联结AE,又知AC⊥ED,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一次函数y=-2x+4,下列结论错误的是( )
A. 函数的图象与x轴的交点坐标是![]()
B. 函数值随自变量的增大而减小
C. 函数的图象不经过第三象限
D. 函数的图象向下平移4个单位长度得![]() 的图象
的图象
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年5月的第二个星期日即为母亲节,“父母恩深重,恩怜无歇时”,许多市民喜欢在母亲节为母亲送鲜花,感恩母亲,祝福母亲. 节日前夕,某花店采购了一批鲜花礼盒,成本价为30元每件,分析上一年母亲节的鲜花礼盒销售情况,得到了如下数据,同时发现每天的销售量![]() (件)是销售单价
(件)是销售单价![]() (元/件)的一次函数.
(元/件)的一次函数.
销售单价 | … | 30 | 40 | 50 | 60 | … |
每天销售量 | … | 350 | 300 | 250 | 200 | … |
(1)求出![]() 与
与![]() 的函数关系;
的函数关系;
(2)物价局要求,销售该鲜花礼盒获得的利润不得高于100﹪:
①当销售单价![]() 取何值时,该花店销售鲜花礼盒每天获得的利润为5000元?(利润=销售总价-成本价);
取何值时,该花店销售鲜花礼盒每天获得的利润为5000元?(利润=销售总价-成本价);
②试确定销售单价![]() 取何值时,花店销该鲜花礼盒每天获得的利润
取何值时,花店销该鲜花礼盒每天获得的利润![]() (元)最大?并求出花店销该鲜花礼盒每天获得的最大利润.
(元)最大?并求出花店销该鲜花礼盒每天获得的最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com