
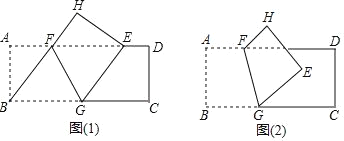
【题目】如图,长方形纸片ABCD中,AB=8,将纸片折叠,折痕的一个端点F在边AD上,另一个端点G在边BC上,顶点B的对应点为E.
(1)如图(1),当顶点B的对应点E落在边AD上时.
①连接BF,试判断四边形BGEF是怎样的特殊四边形,并说明理由;
②若BG=10,求折痕FG的长;
(2)如图(2),当顶点B的对应点E落在长方形内部,E到AD的距离为2,且BG=10时,求AF的长.
【答案】(1)①菱形;②4![]() ;(2)
;(2)![]()
【解析】
(1)①先证明四边形BGEF是平行四边形,再根据BG=EG,即可证得四边形BGEF是菱形;
②如图,过F作FH⊥BC于H,先证明四边形ABHF是矩形,可得FH=AB=8,再由四边形BGEF是菱形,可得BF=BG=10,在Rt△BHF中,利用勾股定理求出BH长,继而求得HG长,在Rt△FHG中,利用勾股定理即可求得FG长;
(2)设EH与AD相交于点K,过点E作MN∥CD分别交AD、BC于M、N,然后求出EM、EN,在Rt△ENG中,利用勾股定理列式求出GN,再根据△GEN和△EKM相似,利用相似三角形对应边成比例列式求出EK、KM,再求出KH,然后根据△FKH和△EKM相似,利用相似三角形对应边成比例列式求解即可.
(1)①四边形BGEF是菱形,理由如下:
∵四边形ABCD是矩形,
∴AD∥BC,BH∥EG,
∴四边形BGEF是平行四边形;
由折叠知,BG=EG,
∴四边形BGEF是菱形;
②如图,过F作FH⊥BC于H,

∵四边形ABCD是矩形,
∴∠A=∠ABC=∠BHF=90°,
∴四边形ABHF是矩形,
∴FH=AB=8,
由①知,四边形BGEF是菱形,
∴BF=BG=10,
在Rt△BHF中,根据勾股定理得,BH=6,
∴HG=BG﹣BH=4,
在Rt△FHG中,根据勾股定理得,FG=![]() =4
=4![]() ;
;
(2)如图,设EH与AD相交于点K,过点E作MN∥CD分别交AD、BC于M、N,
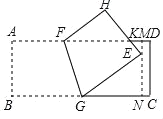
∵E到AD的距离为2,
∴EM=2,EN=8﹣2=6,
在Rt△ENG中,GN=![]() =8,
=8,
∵∠GEN+∠KEM=180°﹣∠GEH=180°﹣90°=90°,
∠GEN+∠NGE=180°﹣90°=90°,
∴∠KEM=∠NGE,
又∵∠ENG=∠KME=90°,
∴△GEN∽△EKM,
∴![]() ,
,
即![]() ,
,
解得EK=![]() ,KM=
,KM=![]() ,
,
∴KH=EH﹣EK=8﹣![]() =
=![]() ,
,
∵∠FKH=∠EKM,∠H=∠EMK=90°,
∴△FKH∽△EKM,
∴![]() ,
,
即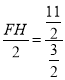 ,
,
解得FH=![]() ,
,
∴AF=FH=![]() .
.


科目:初中数学 来源: 题型:
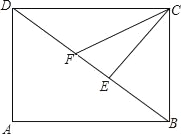
【题目】如图,矩形ABCD中,CE⊥BD于E,CF平分∠DCE与DB交于点F.
(1)求证:BF=BC;
(2)若AB=4cm,AD=3cm,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,学校组织学生去某景点游玩,甲旅行社说:“如果带队的一名老师购买全票,则学生享受半价优惠”; 乙旅行社说:“所有人按全票价的六折优惠”.已知全票价为a元,学生有x人,带队老师有1人.
(1)试用含a和x的式子表示甲、乙旅行社的收费;
(2)若有30名学生参加本次活动,请你为他们选择一家更优惠的旅行社.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )

A. (![]() ,0) B. (2,0) C. (
,0) B. (2,0) C. (![]() ,0) D. (3,0)
,0) D. (3,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,从图中可以看出,终点表示的数是﹣2,已知A,B是数轴上的点.请参照图并思考,完成下列填空:
(1)如果点A表示数3,将点A向右移动7个单位长度,那么终点B表示的数是 ,A,B两点间的距离是 .
(2)如果点B表示数2,将点B向左移动9个单位长度,再向右移动5个单位长度,那么终点A表示的数是 ,A,B两点间的距离是 .

(3)如果点A表示的数是﹣4,将点A向右移动168个单位长度;再向左移动2个单位长度,那么终点B表示的数是 ,A,B两点间的距离是 .
(4)一般地,如果A点表示的数为m,将A点向右移动n个单位长度,再向左移动p个单位长度,那么请你猜想终点B表示的数是 ,A,B两点间的距离是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=50°,∠BAC的角平分线AF与AB的垂直平分线DF交于点F,连接CF,BF,则∠BCF的度数为( )

A. 30°B. 40°C. 50°D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】寻找公式,求代数式的值:从2开始,连续的的偶数相加,它们的和的情况如下表:

(1)根据上面的等式,你能发现当n个连续的的偶数相加时,它们的和S=2+4+6+8+……+2n= .
(2)并按照此规律计算:①2+4+6+……300的值;②162+164+166+……+400的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店欲购进一批跳绳,若同时购进A种跳绳10根和B种跳绳7根,则共需395元,若同时购进A种跳绳5根和B种跳绳3根,共需185元
(1)求A、B两种跳绳的单价各是多少?
(2)若该商店准备同时购进这两种跳绳共100根,且A种跳绳的数量不少于跳绳总数量的![]() .若每根A种跳绳的售价为26元,每根B种跳绳的售价为30元,问:该商店应如何进货才可获取最大利润,并求出最大利润.
.若每根A种跳绳的售价为26元,每根B种跳绳的售价为30元,问:该商店应如何进货才可获取最大利润,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家规定个人发表文章、出版图书所得稿费的纳税计算方法是:
(1)稿费不高于800元的不纳税;
(2)稿费高于800元,而低于4000元的应缴纳超过800元的那部分稿费的14%的税;
(3)稿费为4000元或高于4000元的应缴纳全部稿费的11%的税,
试根据上述纳税的计算方法作答:
①若王老师获得的稿费为2400元,则应纳税________元,若王老师获得的稿费为4000元,则应纳税________元.
②若王老师获稿费后纳税420元,求这笔稿费是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com