
分析 ①先根据反比例函数中k>0判断出函数图象所在的象限及增减性,再根据各点横坐标的特点即可得出结论.
②根据反比例函数图形上点的坐标特征得到y3=-$\frac{3}{a}$,y4=-$\frac{3}{a+1}$,然后分三种情况讨论:当a>0或当-1<a<0或当a<-1.
解答 解:①∵反比例函数y=-$\frac{3}{x}$中k=-3<0,
∴函数图象的两个分式分别位于二、四象限,且在每一象限内y随x的增大而增大.
∵7>5,
∴y1>y2.
②把点C(a,y3),d(a+1,y4)代入y=-$\frac{3}{x}$得a•y3=-3,(a+1)•y4=-3,所以y3=-$\frac{3}{a}$,y4=-$\frac{3}{a+1}$,
当a>0时,y3<y4;当-1<a<0时,y3>y4;当a<-1时,y3<y4,
所以当a>0或a<-1时,y3<y4;当-1<a<0时,y3>y4.
故答案为y1>y2、当a>0或a<-1时,y1<y2;当-1<a<0时,y1>y2.
点评 本题考查了反比例函数图形上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.


科目:初中数学 来源: 题型:解答题
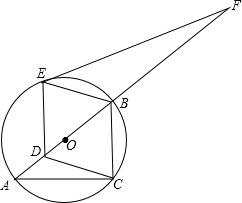 如图,点A,B,C在⊙O上,AB是⊙O的直径,AC=4,BC=3.
如图,点A,B,C在⊙O上,AB是⊙O的直径,AC=4,BC=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,点E是∠ABC、∠ACB角平分线的交点,点F是∠ABC、∠ACB外角平分线的交点,点A1是内角∠ABC、外角∠ACD平分线的交点.
如图,在△ABC中,点E是∠ABC、∠ACB角平分线的交点,点F是∠ABC、∠ACB外角平分线的交点,点A1是内角∠ABC、外角∠ACD平分线的交点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
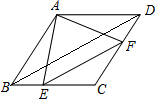 如图,在菱形ABCD中,∠ABC中,∠ABC=60°,点E、F分别从点B、D同时出发,以同样的速度沿边BC、DC向点C运动(点E、F不与点B、D重合).给出以下四个结论:①AE=AF;②EF∥BD;③当点E、F分别为边BC、DC的中点时,EF=$\sqrt{3}$BE;④当点E、F分别为边BC、DC的中点时,△AEF的面积最大.上述结论中正确的个数有( )
如图,在菱形ABCD中,∠ABC中,∠ABC=60°,点E、F分别从点B、D同时出发,以同样的速度沿边BC、DC向点C运动(点E、F不与点B、D重合).给出以下四个结论:①AE=AF;②EF∥BD;③当点E、F分别为边BC、DC的中点时,EF=$\sqrt{3}$BE;④当点E、F分别为边BC、DC的中点时,△AEF的面积最大.上述结论中正确的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com