
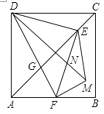
【题目】如图,正方形 ABCD 中,AD=6,点 E 是对角线 AC 上一点,连接 DE,过点 E 作 EF⊥ ED,交 AB 于点 F,连接 DF,交 AC 于点 G,将△EFG 沿 EF 翻折,得到△EFM,连接DM,交 EF 于点 N,若点 F 是 AB 边的中点,则 △EDM 的面积是_____.
【答案】![]()
【解析】
取DF的中点K,连接AK,KE,GM,得出点D、A、F、E四点共圆,进而得出△DEF是等腰直角三角形,通过已知数据计算出DF,DE,EF的长度,再由相似得出GF,由折叠的性质得到△GFM是等腰直角三角形,进而计算出MH,EH的长度,由△DEN∽△MHN得到EH的长度,最后由![]() 即可计算.
即可计算.
解:取DF的中点K,连接AK,KE,GM,
∵四边形ABCD是正方形,DE⊥EF,
∴∠DAF=90°,∠DAC=45°,
∴AK=![]() ,EK=
,EK=![]() ,
,
∴点D、A、F、E四点共圆,
∴∠DFE=∠DAC=45°(同弧所对的圆周角相等),
∴△DEF是等腰直角三角形,
又∵AD=6,点 F 是 AB 边的中点,
∴AF=3,DF=![]() ,
,
∴DE=EF=![]() ,
,
又∵AF∥DC
△AGF∽△CGD
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
又∵△EFM是由△EFG翻折得到,
∴GM⊥EF,∠EFG=∠EFM=45°,GF=MF
∴△GFM是等腰直角三角形,
∴GM=![]() ,
,
∴MH=FH=![]() ,
,
∴EH=EF-FH=![]()
又∵DE⊥EF,MH⊥EF,
∴△DEN∽△MHN
∴![]() ,即
,即
∴![]() ,
,
∴![]() ,
,
![]()
![]()
=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=﹣x﹣1的图象与x轴交于点A,与y轴交于点B,与反比例函数![]() 图象的一个交点为M(﹣2,m).
图象的一个交点为M(﹣2,m).
(1)求反比例函数的解析式;(2)求点B到直线OM的距离.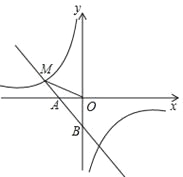
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】倡导健康生活推进全民健身,某社区去年购进A,B两种健身器材若干件,经了解,B种健身器材的单价是A种健身器材的1.5倍,用7200元购买A种健身器材比用5400元购买B种健身器材多10件.
(1)A,B两种健身器材的单价分别是多少元?
(2)若今年两种健身器材的单价和去年保持不变,该社区计划再购进A,B两种健身器材共50件,且费用不超过21000元,请问:A种健身器材至少要购买多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线y=![]() x﹣3与x轴、y轴分别交于点A、B,抛物线y=
x﹣3与x轴、y轴分别交于点A、B,抛物线y=![]() x2+bx+c经过点A、B,且交x轴于点C.
x2+bx+c经过点A、B,且交x轴于点C.
(1)求抛物线的解析式;
(2)点P为抛物线上一点,且点P在AB的下方,设点P的横坐标为m.
①试求当m为何值时,△PAB的面积最大;
②当△PAB的面积最大时,过点P作x轴的垂线PD,垂足为点D,问在直线PD上否存在点Q,使△QBC为直角三角形?若存在,直接写出符合条件的Q的坐标若不存在,请说明理由.
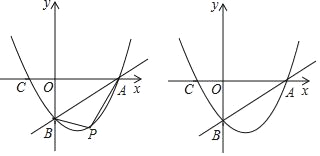
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为∠ABC的边![]() 上的一点,过点O作OM⊥AB于点
上的一点,过点O作OM⊥AB于点![]() ,到点
,到点![]() 的距离等于线段OM的长的所有点组成图形
的距离等于线段OM的长的所有点组成图形![]() .图形W与射线
.图形W与射线![]() 交于E,F两点(点在点F的左侧).
交于E,F两点(点在点F的左侧).
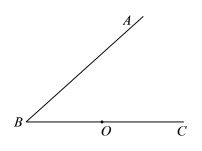
(1)过点![]() 作
作![]() 于点
于点![]() ,如果BE=2,
,如果BE=2,![]() ,求MH的长;
,求MH的长;
(2)将射线BC绕点B顺时针旋转得到射线BD,使得∠![]()
![]() ,判断射线BD与图形
,判断射线BD与图形![]() 公共点的个数,并证明.
公共点的个数,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲地到乙地有A,B,C三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
公交车用时 公交车用时的频数 线路 |
|
|
|
| 合计 |
A | 59 | 151 | 166 | 124 | 500 |
B | 50 | 50 | 122 | 278 | 500 |
C | 45 | 265 | 167 | 23 | 500 |
早高峰期间,乘坐_________(填“A”,“B”或“C”)线路上的公交车,从甲地到乙地“用时不超过45分钟”的可能性最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
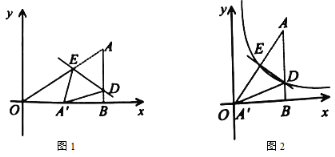
【题目】如图1,点A在第一象限,![]() 轴于B点,连结
轴于B点,连结![]() ,将
,将![]() 折叠,使
折叠,使![]() 点落在x轴上,折痕交
点落在x轴上,折痕交![]() 边于D点,交斜边
边于D点,交斜边![]() 于E点,(1)若A点的坐标为
于E点,(1)若A点的坐标为![]() ,当
,当![]() 时,点
时,点![]() 的坐标是______;(2)若
的坐标是______;(2)若![]() 与原点O重合,
与原点O重合,![]() ,双曲线
,双曲线![]() 的图象恰好经过D,E两点(如图2),则
的图象恰好经过D,E两点(如图2),则![]() ____.
____.
查看答案和解析>>
科目:初中数学 来源: 题型:
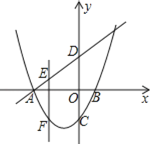
【题目】如图,抛物线y=ax2+bx﹣1(a≠0)交x轴于A,B(1,0)两点,交y轴于点C,一次函数y=x+3的图象交坐标轴于A,D两点,E为直线AD上一点,作EF⊥x轴,交抛物线于点F
(1)求抛物线的解析式;
(2)若点F位于直线AD的下方,请问线段EF是否有最大值?若有,求出最大值并求出点E的坐标;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
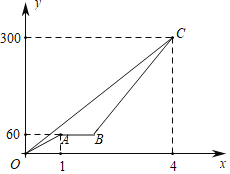
【题目】甲车与乙车同时从A地出发去往B地,如图所示,折线O﹣A﹣B﹣C和射线OC分别是甲、乙两车行进过程中路程与时间的关系,已知甲车中途有事停留36分钟后再继续前往C地,两车同时到达C地,则下列说法:①乙车的速度为70千米/时;②甲车再次出发后的速度为100千米/时;③两车在到达B地前不会相遇;④甲车再次出发时,两车相距60千米.其中正确的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com