
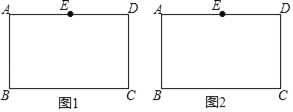
【题目】如图,在矩形ABCD中,点E为AD的中点,不用圆规、量角器等工具,只用无刻度的直尺作图.
(1)如图1,在BC上找点F,使点F是BC的中点;
(2)如图2,连接AC,在AC上取两点P,Q,使P,Q是AC的三等分点.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)根据矩形的对角线相等且互相平分作出图形即可;
(2)根据矩形的性质和三角形中位线定理作出图形即可.
(1)如图1,连接AC、BD交于点O,延长EO交BC于F,则点F即为所求.
证明如下:
∵ABCD是矩形,
∴BO=OD,AD∥BC,AD=BC,
∴∠EDO=∠FBO.
∵∠EOD=∠FOB,
∴△EOD≌△FOB,
∴ED=FB=![]() AD=
AD=![]() BC,
BC,
∴F为BC的中点.
(2)如图2,BD交AC于O,延长EO交BC于F.
连接EB交AC于P,连接DF交AC于Q,则P、Q即为所求.
证明如下:
由(1)可得:F为BC的中点,
∴ED=BF=AE=FC,ED∥BF,
∴四边形EBFD是平行四边形,
∴BE∥FD.
∵FC=BF,
∴CQ=PQ.
∵AD∥BC,
∴∠EAC=∠FCA,∠ADQ=∠CFQ.
∵BE∥FD,
∴∠AEP=∠ADQ,
∴∠AEP=∠CFQ.
在△AEP和△CFQ中,
∵∠EAC=∠FCA,AE=CF,∠AEP=∠CFQ,
∴△AEP≌△CFQ,
∴AP=CQ,
∴AP=PQ=CQ,
∴P,Q是AC的三等分点.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】把函数C1:y=ax2﹣2ax﹣3a(a≠0)的图象绕点P(m,0)旋转180°,得到新函数C2的图象,我们称C2是C1关于点P的相关函数.C2的图象的对称轴与x轴交点坐标为(t,0).
(1)填空:t的值为 (用含m的代数式表示)
(2)若a=﹣1,当![]() ≤x≤t时,函数C1的最大值为y1,最小值为y2,且y1﹣y2=1,求C2的解析式;
≤x≤t时,函数C1的最大值为y1,最小值为y2,且y1﹣y2=1,求C2的解析式;
(3)当m=0时,C2的图象与x轴相交于A,B两点(点A在点B的右侧).与y轴相交于点D.把线段AD原点O逆时针旋转90°,得到它的对应线段A′D′,若线A′D′与C2的图象有公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.
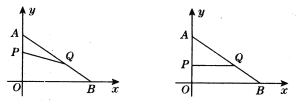
(1)求直线AB的解析式;
(2)当t为何值时,△APQ与△AOB相似?
(3)当t为何值时,△APQ的面积为![]() 个平方单位?
个平方单位?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 经过点
经过点![]() 和点
和点![]() ,顶点为
,顶点为![]() .
.
(1)求这条抛物线的表达式和顶点![]() 的坐标;
的坐标;
(2)点![]() 关于抛物线对称轴的对应点为点
关于抛物线对称轴的对应点为点![]() ,联结
,联结![]() ,求
,求![]() 的正切值;
的正切值;
(3)将抛物线![]() 向上平移
向上平移![]() 个单位,使顶点
个单位,使顶点![]() 落在点
落在点![]() 处,点
处,点![]() 落在点
落在点![]() 处,如果
处,如果![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养殖场计划用96米的竹篱笆围成如图所示的①、②、③三个养殖区域,其中区域①是正方形,区域②和③是矩形,且AG∶BG=3∶2.设BG的长为2x米.
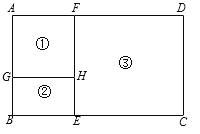
(1)用含x的代数式表示DF= ;
(2)x为何值时,区域③的面积为180平方米;
(3)x为何值时,区域③的面积最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a#0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0).下列结论:①ab<0;②b2>4ac;③0<b<1;④当x<﹣1时,y<0.其中正确结论的个数是( )
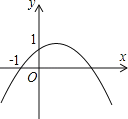
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,关于x的方程:x+![]() =c+
=c+![]() 的解是x1=c,x2=
的解是x1=c,x2=![]() ;x﹣
;x﹣![]() =c﹣
=c﹣![]() 的解是x1=c,x2=﹣
的解是x1=c,x2=﹣![]() ;x+
;x+![]() =c+
=c+![]() 的解是x1=c,x2=
的解是x1=c,x2=![]() ;x+
;x+![]() =c+
=c+![]() 的解是x1=c,x2=
的解是x1=c,x2=![]() ;……
;……
(1)请观察上述方程与解的特征,比较关于x的方程x+![]() =c+
=c+![]() (a≠0)与它们的关系猜想它的解是什么,并利用“方程的解”的概念进行验证.
(a≠0)与它们的关系猜想它的解是什么,并利用“方程的解”的概念进行验证.
(2)可以直接利用(1)的结论,解关于x的方程:x+![]() =a+
=a+![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明经过市场调查,整理出他妈妈商店里一种商品在第![]() 天的销售量的相关信息如下表:
天的销售量的相关信息如下表:
时间第 |
|
|
售价(元/件) |
| 50 |
每天销量(件) |
| |
已知该商品的进价为每件20元,设销售该商品的每天利润为![]() 元.
元.
(1)求出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于2400元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地盛产樱桃,一年一度的樱桃节期间,很多果园推出了免费品尝和优惠采摘活动,其中甲、乙两家果园的樱桃品质相同,销售价格也相同,但推出了不同的采摘方案:
甲园 | 游客进园需购买 |
乙园 | 游客进园不需购买门票,采摘的樱桃在一定数量以内按原价购买,超过部分打折购买 |
小明和爸爸、妈妈在樱桃节期间也来采摘樱桃,若设他们的樱桃采摘量为![]() (千克)(出园时将自己采摘的樱桃全部购买),在甲采摘园所需总费用为
(千克)(出园时将自己采摘的樱桃全部购买),在甲采摘园所需总费用为![]() (元)在乙采摘园所需总费用为
(元)在乙采摘园所需总费用为![]() (元),图中的折线
(元),图中的折线![]() 表示
表示![]() 与
与![]() 之间的函数关系.
之间的函数关系.

(1)①甲、乙两果园的樱桃单价为_____________元![]() 千克;
千克;
②直接写出![]() 的函数表达式:_________________,并在图中补画出
的函数表达式:_________________,并在图中补画出![]() 的函数图象;
的函数图象;
(2)求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)若小明一家当天所采摘的樱桃不少于![]() 千克,选择哪个采摘园更划算?请说明理由.
千克,选择哪个采摘园更划算?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com