Question

8．△ABC中，点D在边BC上，已知AB=AD=2，AC=4，且BD：DC=2：3，则△ABC是（　　）

• A． 锐角三角形
• B． 直角三角形
• C． 钝角三角形
• D． 无法确定

Answer 1

分析 过A作AE⊥BD，设BD=2x，CD=3x，根据等腰三角形的性质可得BE=ED=x，再根据勾股定理可得4²-（x+3x）²=2²-x²，解方程可得x的值，进而可得BC长，再利用勾股定理逆定理可得△ABC是直角三角形．

解答 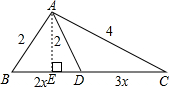解：过A作AE⊥BD，
∵BD：DC=2：3，
∴设BD=2x，CD=3x，
∵AB=AD，AE⊥BD，
∴BE=ED=x，
由勾股定理可得：4²-（x+3x）²=2²-x²，
解得：$x=\frac{{2\sqrt{5}}}{5}$，
∴$BC=2\sqrt{5}$，
∵2²+4²=（2$\sqrt{5}$）²，
∴△ABC是直角三角形，
故选：B．

点评 此题主要考查了勾股定理逆定理，关键是正确画出图形，作出辅助线，利用勾股定理计算出BC长．