
【题目】如图,等腰三角形ABC的底边BC在x轴正半轴上,点A在第一象限,延长AB交y轴负半轴于点D,延长CA到点E,使AE=AC,双曲线y= ![]() (x>0)的图象过点E.若△BCD的面积为2
(x>0)的图象过点E.若△BCD的面积为2 ![]() ,则k的值为( )
,则k的值为( )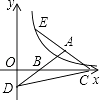
A.4 ![]()
B.4
C.2 ![]()
D.2
【答案】A
【解析】解:如图,连接BE,
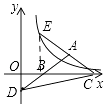
∵等腰三角形ABC中,AB=AC,
∴∠ABC=∠ACB,
∵AE=AC,
∴AE=AB,
∴∠AEB=∠ABE,
又∵∠AEB+∠ABE+∠ABC+∠ACB=180°,
∴∠ABE+∠ABC=90°,即BE⊥BC,
∴∠CBE=∠BOD=90°,
又∵∠ACB=∠ABC=∠OBD,
∴△CBE∽△BOD,
∴ ![]() =
= ![]() ,即BC×OD=OB×BE,
,即BC×OD=OB×BE,
又∵△BCD的面积为2 ![]() ,
,
∴BC×OD=4 ![]() ,
,
∴OB×BE=4 ![]() ,
,
又∵双曲线y= ![]() (x>0)的图象过点E,
(x>0)的图象过点E,
∴k=OB×BE=4 ![]() ,
,
所以答案是:A.
【考点精析】利用比例系数k的几何意义和等腰三角形的性质对题目进行判断即可得到答案,需要熟知几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积;等腰三角形的两个底角相等(简称:等边对等角).


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,点O在∠APB的平分线上,⊙O与PA相切于点C.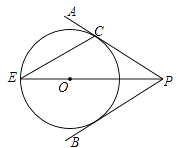
(1)求证:直线PB与⊙O相切;
(2)PO的延长线与⊙O交于点E.若⊙O的半径为3,PC=4.求弦CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为原点,一次函数y1=x+m与反比例函数y2= ![]() 的图象相交于A(2,1),B(n,﹣2)两点,与x轴交于点C.
的图象相交于A(2,1),B(n,﹣2)两点,与x轴交于点C.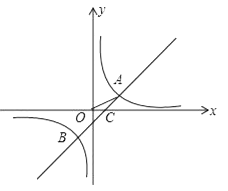
(1)求反比例函数解析式和点B坐标;
(2)当x的取值范围是时,有y1>y2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设M(m,n)在反比例函数y=﹣ ![]() 上,其中m是分式方程
上,其中m是分式方程 ![]() ﹣1=
﹣1= ![]() 的根,将M点先向上平移4个单位,再向左平移1个单位,得到点N.若点M,N都在直线y=kx+b上,直线解析式为( )
的根,将M点先向上平移4个单位,再向左平移1个单位,得到点N.若点M,N都在直线y=kx+b上,直线解析式为( )
A.y=﹣ ![]() x﹣
x﹣ ![]()
B.y= ![]() x+
x+ ![]()
C.y=4x﹣5
D.y=﹣4x+5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题 1、如图1,线段AB的端点在正方形网格的格点上,在图1中找到格点C,使组成的△ABC的一个内角α满足tanα=2(找到两个点C,全等的三角形算一种)
2、
(1)如图1,线段AB的端点在正方形网格的格点上,在图1中找到格点C,使组成的△ABC的一个内角α满足tanα=2(找到两个点C,全等的三角形算一种).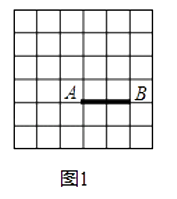
(2)如图2,在Rt△DEF中,∠DEF=90°,DE=1,sin∠F= ![]() .用两块全等的△DEF拼出一个平行四边形,将拼得的平行四边形画在图2网格(网格图中小正方形边长均为1)中,画出不同的两种平行四边形(全等的算一种),并写出相应的周长.
.用两块全等的△DEF拼出一个平行四边形,将拼得的平行四边形画在图2网格(网格图中小正方形边长均为1)中,画出不同的两种平行四边形(全等的算一种),并写出相应的周长.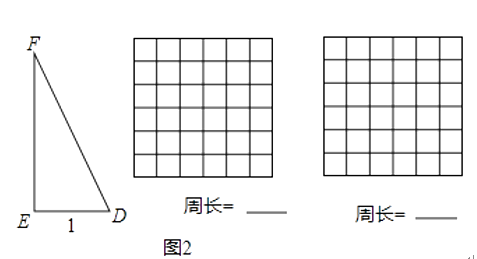
查看答案和解析>>
科目:初中数学 来源: 题型:
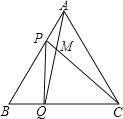
【题目】点P、Q分别是边长为4cm的等边![]() 的边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都是
的边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都是![]() ,设运动时间为t秒.
,设运动时间为t秒.
![]() 连接AQ、CP交于点M,则在P、Q运动的过程中,
连接AQ、CP交于点M,则在P、Q运动的过程中,![]() 变化吗:若变化,则说明理由,若不变,则求出它的度数;
变化吗:若变化,则说明理由,若不变,则求出它的度数;
![]() 连接PQ,
连接PQ,
![]() 当
当![]() 秒时,判断
秒时,判断![]() 的形状,并说明理由;
的形状,并说明理由;
![]() 当
当![]() 时,则
时,则![]() ______秒
______秒![]() 直接写出结果
直接写出结果![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2)
(1)观察图2请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 ;
(2)根据(1)中的结论,若x+y=5,xy=![]() ,则x﹣y= ;
,则x﹣y= ;
(3)拓展应用:若(2019﹣m)2+(m﹣2020)2=15,求(2019﹣m)(m﹣2020)的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com