
【题目】如图,![]() 与⊙
与⊙![]() 相切于点
相切于点![]() ,
,![]() 为⊙
为⊙![]() 的弦,
的弦,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.

【答案】(1) 证明见解析;(2) ![]() .
.
【解析】
(1)根据已知条件,结合同角的余角相等的性质易证∠APB=∠ABP,即可证得AP=AB;(2)作OH⊥BC于H.在Rt△OAB中,根据勾股定理求得OA的长;在Rt△POC中,根据勾股定理求得PC的长;再利用直角三角形面积的两种表示法求得OH的长,在Rt△OCH中,根据勾股定理求得求得CH的长;利用垂径定理求得BC的长,即可求得PB的长.
(1)证明:∵OC=OB,
∴∠OCB=∠OBC,
∵AB是⊙O的切线,
∴OB⊥AB,
∴∠OBA=90°,
∴∠ABP+∠OBC=90°,
∵OC⊥AO,
∴∠AOC=90°,
∴∠OCB+∠CPO=90°,
∵∠APB=∠CPO,
∴∠APB=∠ABP,
∴AP=AB.
(2)作OH⊥BC于H.
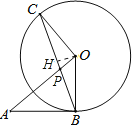
在Rt△OAB中, OB=4,AB=3,根据勾股定理求得OA=5,
∵AP=AB=3,
∴PO=2.
在Rt△POC中,根据勾股定理求得PC=2![]() .
.
∵![]() PCOH=
PCOH=![]() OCOP,
OCOP,
∴OH=![]() ,
,
∴CH=![]() ,
,
∵OH⊥BC,
∴CH=BH,
∴BC=2CH=![]() ,
,
∴PB=BC-PC=![]() -2
-2![]() =
=![]() .
.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,﹣1),与x轴以及y=x+1的图象分别交于点C、D,且点D的坐标为(1,n),
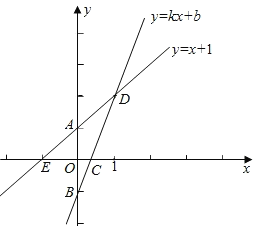
(1)求一次函数y=kx+b的函数关系式
(2)求四边形AOCD的面积;
(3)是否存在y轴上的点P,使得以BD为底的△PBD等腰三角形?若存在求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,射线AP在△ABC的外侧,点B关于AP的对称点为D,连接CD交射线AP于点E,连接BE.
(1)根据题意补全图形;
(2)求证:CD=EB+EC;
(3)求证:∠ABE=∠ACE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如![]() .善于思考的小明进行了以下探索:
.善于思考的小明进行了以下探索:
设![]() (其中
(其中![]() 、
、![]() 、
、![]() 、
、![]() 均为整数),则有
均为整数),则有![]() .
.
∴![]() ,
,![]() .这样小明就找到了一种把类似
.这样小明就找到了一种把类似![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法解决下列问题:
(1)当![]() 、
、![]() 、
、![]() 、
、![]() 均为正整数时,若
均为正整数时,若![]() ,用含
,用含![]() 、
、![]() 的式子分别表示
的式子分别表示![]() 、
、![]() ,得
,得![]() _________,
_________,![]() _________.
_________.
(2)利用所探索的结论,填空:![]() (_____+_____
(_____+_____![]() )2;
)2;
(3)若![]() ,且
,且![]() 、
、![]() 、
、![]() 均为正整数,求
均为正整数,求![]() 的值?
的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为______.
周长的最小值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:要将一块直径为![]() 的半圆形铁皮加工成一个圆柱的两个底面和一个圆锥的底面.
的半圆形铁皮加工成一个圆柱的两个底面和一个圆锥的底面.

操作:
方案一:在图![]() 中,设计一个圆锥底面最大,半圆形铁皮得以最充分利用的方案(要求:画示意图);
中,设计一个圆锥底面最大,半圆形铁皮得以最充分利用的方案(要求:画示意图);
方案二:在图![]() 中,设计一个圆柱两个底面最大,半圆形铁皮得以最充分利用的方案(要求:画示意图).
中,设计一个圆柱两个底面最大,半圆形铁皮得以最充分利用的方案(要求:画示意图).
探究:
![]() 求方案一中圆锥底面的半径;
求方案一中圆锥底面的半径;
![]() 求方案二中半圆圆心为
求方案二中半圆圆心为![]() ,圆柱两个底面圆心为
,圆柱两个底面圆心为![]() 、
、![]() ,圆锥底面的圆心为
,圆锥底面的圆心为![]() ,试判断以
,试判断以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是什么样的特殊四边形,并加以证明.
为顶点的四边形是什么样的特殊四边形,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要建一个面积为150平方米的长方形养鸡场,为了节约材料,鸡场一边靠着原有的一堵墙,墙长为18米,另三边用篱笆围成,如篱笆长度为35米,且要求用完。求鸡场的长与宽各是多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1;(要求:A与A1,B与B1,C与C1相对应)
(2)在(1)问的结果下,连接BB1,CC1,求四边形BB1C1C的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com