
 有一座小型三塘的塘坝横截面是一个等腰梯形,上底宽为1.2米,坡长为3米,坡度i=$\sqrt{3}:1$,求塘坝的横截面积.($\sqrt{3}$=1.732,计算结果精确到0.01)
有一座小型三塘的塘坝横截面是一个等腰梯形,上底宽为1.2米,坡长为3米,坡度i=$\sqrt{3}:1$,求塘坝的横截面积.($\sqrt{3}$=1.732,计算结果精确到0.01) 分析 分别过点A、D作AE⊥BC于点E、DF⊥BC于点F,根据坡长AB=3米,坡度i=$\sqrt{3}:1$,求出BE和AE的长度,同理可得出DF、CF的长度,继而可求得塘坝的横截面积.
解答 解: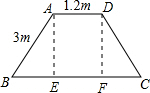 过点A、D作AE⊥BC于点E、DF⊥BC于点F,
过点A、D作AE⊥BC于点E、DF⊥BC于点F,
则四边形AEFD为矩形,AD=EF=1.2m,
在Rt△ABE中,
∵AB=3米,坡度i=$\sqrt{3}:1$,
∴设AE=$\sqrt{3}$x,BE=x,
则有:($\sqrt{3}$x)2+x2=9,
解得:x=$\frac{3}{2}$,
则AE=$\frac{3}{2}$$\sqrt{3}$米,BE=$\frac{3}{2}$米,
同理可得,DF=$\frac{3}{2}$$\sqrt{3}$米,FC=$\frac{3}{2}$米,
∴塘坝的横截面积为:(1.2+1.2+$\frac{3}{2}$+$\frac{3}{2}$)×$\frac{3}{2}$$\sqrt{3}$÷2≈7.01(平方米).
答:塘坝的横截面积约为7.01平方米.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据坡度和坡角构造直角三角形,注意掌握等腰三角形的性质.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com