
| 3 |
| 3 |
| 3 |
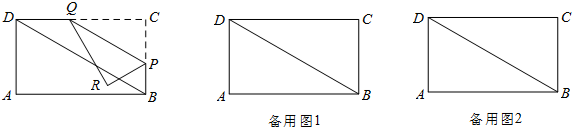
| BC |
| CD |
| ||
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 3 |
| ||
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
3
| ||
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
|


科目:初中数学 来源: 题型:
 (2012•滨海县二模)如图,数表有7行7列,设aij表示第i行第j列上的数,例如:a36表示第3行第6列上的数,即a36=4.则(a23-a22)+(a52-a53)=
(2012•滨海县二模)如图,数表有7行7列,设aij表示第i行第j列上的数,例如:a36表示第3行第6列上的数,即a36=4.则(a23-a22)+(a52-a53)=查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解

| 图书种类 | 频数 | 频率 |
| 科普常识 | B | 0.2 |
| 名人传记 | 500 | 0.25 |
| 中外名著 | 800 | A |
| 其 它 | 300 | 0.15 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (注意:如果指针恰好指在分割线上,那么重转一次,直到指针指向某一区域为止).
(注意:如果指针恰好指在分割线上,那么重转一次,直到指针指向某一区域为止).查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•滨海县二模)如图所示,AB是⊙O的直径,AB=4,D是⊙O上的一点,∠ABD=30°,OF∥AD交BD于点E,交⊙O于点F.
(2012•滨海县二模)如图所示,AB是⊙O的直径,AB=4,D是⊙O上的一点,∠ABD=30°,OF∥AD交BD于点E,交⊙O于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com