练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．在一只底面积为6.28平方厘米装有水的圆柱形玻璃杯里，完全浸没一块底面积为3.14平方厘米的圆锥形铁块．从杯中取出铁块后，杯里的水面下降了1厘米，这块圆锥形铁块的高是多少厘米？

    分析 上升1厘米的水的体积就是底面积为3.14平方厘米的圆锥的体积，由此利用圆锥的体积公式求出上升的水的体积，再利用圆锥的高=体积×3÷底面积，求圆锥的高．

    解答 解：6.28×1×3÷3.14 
    =6.28×3÷3.14 
    =6（厘米）． 
    答：这块圆锥形铁块的高是6厘米．

    点评 此题考查了圆柱与圆锥的体积公式的综合应用，这里根据题干得出圆锥的体积=上升部分水的体积是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    3．对于两个相似三角形，如果沿周界按对应点顺序环绕方向相同，那么称这两个三角形互为顺相似；如果沿周界按对应点顺序环绕的方向相反，那么称这两个三角形互为逆相似．例如：
    如图①，△ABC∽△A′B′C′，且沿周界ABCA与A′B′C′A′环绕的方向相同，因此△ABC与△A′B′C′互为顺相似；
    如图②△ABC∽△A′B′C′，且沿周界ABCA与A′B′C′A′环绕的方向相反，因此△ABC与△A′B′C′互为逆相似；

    （1）根据图Ⅰ、图Ⅱ、图Ⅲ满足的条件，可分别得下列三对相似三角形：
    ①△ADE与△ABC；②△FGH与△FNM③△OSK与△OQP．其中，互为顺相似的是①；互为逆相似的是②③．（填写所有符合要求的序号）

    （2）如图在锐角△ABC中，∠A＜∠B＜∠C，点P在△ABC的边上（不与A、B、C重合）过点P画直线截△ABC，使截得的一个三角形与△ABC互为逆相似，画出图形并说明截线满足的条件，不必说明理由．（请至少画出三种截法）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．在Rt△ABC中，CD是斜边AB上的高线，DE⊥AC于E，DF⊥BC于F，求证：$\frac{B{C}^{3}}{A{C}^{3}}$=$\frac{BF}{AE}$．

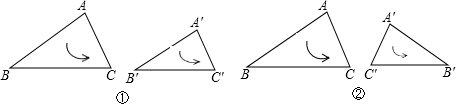
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．已知点P是矩形ABCD内一点，连结AP、BP、CP、DP，若S△ABP+S△CDP=S△ADP+S△BCP，则关于点P的位置，正确的说法是（　　）
    A．一定是对角线交点B．一定在对角线上
    C．一定在对边中点的连线上D．可以是任意位置

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．填空：
    （1）$\frac{m+n}{{m}^{2}{-n}^{2}}$=$\frac{1}{（）}$；
    （2）$\frac{{a}^{2}-2ab{+b}^{2}}{{a}^{2}{-b}^{2}}$=$\frac{（）}{a+b}$；
    （3）$\frac{x+y}{3y}$=$\frac{{x}^{2}{-y}^{2}}{（）}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．一支考古队发现一个残破的古代圆盘碎片，如图所示，考古家测量了弦AB=300mm，圆弧的高为90mm，于是得到了古圆盘的半径，从而确定了它的圆心，终于使这个古物得以复原，请问你知道考古家怎样得到它的半径吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，MA⊥AB于A，NB⊥AB于B，点O是AB的中点，点D是BN上一点，且BD=AO，点C是AM上一点，∠COD=α．
    （1）如图1，若AC=AO，则OC与OD的数量关系为OC=OD，
        α=90°；
    （2）在（1）的条件下，若点P为BN上一点，连接OP，将线段OP以点O为旋转中心，逆时针旋转90°，得到线段OQ，连接CQ，在图2中补全图形．请猜想CQ与DP的数量关系，并证明你的结论．
    （3）在（2）的条件下，若∠OQC=30°，OC=$\sqrt{2}a$，则CQ=（$\sqrt{3}$-1）a（用含α的代数式表示）．

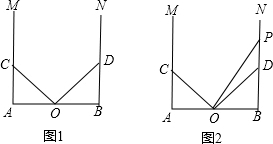
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．已知一直角三角形的木版，三边的平方和为1800cm2，则斜边长为（　　）
    A．80mB．30mC．90mD．120m

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．下列叙述中，错误的是（　　）
    A．代数式x2+y2的意义是x、y两数的平方和
    B．代数式5（x+y）的意义是5与x+y的积
    C．代数式5x+$\frac{y}{2}$的意义是x的5倍与y的和的一半
    D．代数式$\frac{1}{2}$x-$\frac{1}{3}$y的意义是x的$\frac{1}{2}$与y的$\frac{1}{3}$的差

    查看答案和解析>>

    同步练习册答案