
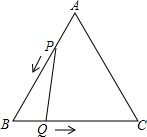
 如图,已知△ABC是边长为3cm的等边三角形,动点P,Q同时从A,B两点出发,分别沿AB,BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P,Q两点都停止运动,设点P的运动时间为t(s).解答下列问题:
如图,已知△ABC是边长为3cm的等边三角形,动点P,Q同时从A,B两点出发,分别沿AB,BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P,Q两点都停止运动,设点P的运动时间为t(s).解答下列问题:分析 (1)根据题意得AP=tcm,BQ=tcm,由PQ∥AC,得到△BPQ∽△BAC,根据相似三角形的性质得到$\frac{PB}{AB}=\frac{BQ}{BC}$,列方程即可得到结论;
(2)根据等边三角形的性质可以知道这个直角三角形∠B=60°,所以就可以表示出BQ与PB的关系,要分情况进行讨论:①∠BPQ=90°;②∠BQP=90°.然后在直角三角形BQP中根据BP,BQ的表达式和∠B的度数进行求解即可.
解答 解:(1)根据题意得AP=tcm,BQ=tcm,
∵PQ∥AC,
∴△BPQ∽△BAC,
∴$\frac{PB}{AB}=\frac{BQ}{BC}$,
即$\frac{3-t}{3}=\frac{t}{3}$,
解得:t=$\frac{3}{2}$,
∴当t=$\frac{3}{2}$时,PQ∥AC;
(2)根据题意得AP=tcm,BQ=tcm,
在△ABC中,∵AB=BC=3cm,∠B=60°,
∴BP=(3-t)cm,
在△PBQ中,BP=3-t,BQ=t,若△PBQ是直角三角形,则∠BQP=90°或∠BPQ=90°,
①当∠BQP=90°时,BQ=$\frac{1}{2}$BP,
即t=$\frac{1}{2}$(3-t),t=1(秒),
②当∠BPQ=90°时,BP=$\frac{1}{2}$BQ,
即3-t=$\frac{1}{2}$t,t=2(秒).
综上所述:当t=1秒或t=2秒时,△PBQ是直角三角形.
点评 本题考查了相似三角形的判定和性质,直角三角形的判定,等边三角形的性质,熟练掌握相似三角形的判定和性质是解题的关键.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知P(-2,1).(第(1)(2)要求保留必要的作图轨迹和简单的说理)
已知P(-2,1).(第(1)(2)要求保留必要的作图轨迹和简单的说理) 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知?ABCD(如图),将它沿AB方向平移,平移的距离为$\frac{1}{2}$AB.
已知?ABCD(如图),将它沿AB方向平移,平移的距离为$\frac{1}{2}$AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
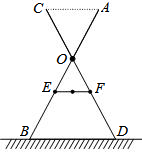 如图是一晒衣架的侧面示意图,立杆AB,CD相交于点O,B,D两点立于地面,经测量:OE=OF=34cm,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=32cm,求扣链EF与立杆AB的夹角∠OEF的度数.(精确到0.1°,可使用科学计算器)
如图是一晒衣架的侧面示意图,立杆AB,CD相交于点O,B,D两点立于地面,经测量:OE=OF=34cm,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=32cm,求扣链EF与立杆AB的夹角∠OEF的度数.(精确到0.1°,可使用科学计算器)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=-$\frac{1}{2}$x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0),C(0,2).
如图,抛物线y=-$\frac{1}{2}$x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0),C(0,2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com