
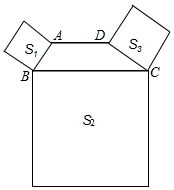
 如图,四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,以AB、BC、DC为边向外作正方形,其面积分别为S1、S2、S3,若S1=3,S3=9,则S2的值为( )
如图,四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,以AB、BC、DC为边向外作正方形,其面积分别为S1、S2、S3,若S1=3,S3=9,则S2的值为( )| A. | 12 | B. | 18 | C. | 24 | D. | 48 |
分析 根据已知条件得到AB=$\sqrt{3}$,CD=3,过A作AE∥CD交BC于E,则∠AEB=∠DCB,根据平行四边形的性质得到CE=AD,AE=CD=3,由已知条件得到∠BAE=90°,根据勾股定理得到BE=$\sqrt{A{B}^{2}+A{E}^{2}}$=2$\sqrt{3}$,于是得到结论.
解答 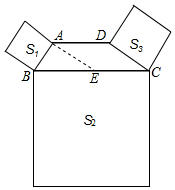 解:∵S1=3,S3=9,
解:∵S1=3,S3=9,
∴AB=$\sqrt{3}$,CD=3,
过A作AE∥CD交BC于E,
则∠AEB=∠DCB,
∵AD∥BC,
∴四边形AECD是平行四边形,
∴CE=AD,AE=CD=3,
∵∠ABC+∠DCB=90°,
∴∠AEB+∠ABC=90°,
∴∠BAE=90°,
∴BE=$\sqrt{A{B}^{2}+A{E}^{2}}$=2$\sqrt{3}$,
∵BC=2AD,
∴BC=2BE=4$\sqrt{3}$,
∴S2=(4$\sqrt{3}$)2=48,
故选D.
点评 本题考查了勾股定理,正方形的性质,平行四边形的判定和性质,正确的作出辅助线是解题的关键.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,这是某市部分简图(图中小正方形的边长代表1km长).以火车站为坐标原点建立平面直角坐标系.
如图,这是某市部分简图(图中小正方形的边长代表1km长).以火车站为坐标原点建立平面直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com