
【题目】如图,在△ABC和△ADE中,点E在BC边上,∠BAC=∠DAE,∠B=∠D, AB=AD.
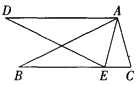
(1)试说明△ABC≌△ADE;
(2)如果∠AEC=75°,将△ADE绕点A旋转一个锐角后与△ABC重合,求这个旋转角的大小.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在梯形ABCD中,AD∥BC,∠ABC=90°,对角线AC、BD相交于点O.下列条件中,不能判断对角线互相垂直的是( ) 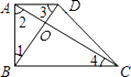
A.∠1=∠4
B.∠1=∠3
C.∠2=∠3
D.OB2+OC2=BC2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小聪和小明沿同一条笔直的马路同时从学校出发到某图书馆查阅资料,学校与 图书馆的路程是 ![]() 千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到 达图书馆,图中折线
千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到 达图书馆,图中折线 ![]() 和线段
和线段 ![]() 分别表示两人离学校的路程
分别表示两人离学校的路程 ![]() (千米)与所经过的 时间
(千米)与所经过的 时间 ![]() (分钟)之间的函数关系,请根据图像回答下列问题:
(分钟)之间的函数关系,请根据图像回答下列问题:
(1)小聪在图书馆查阅资料的时间为 分钟;小聪返回学校的速度为 千米/分钟.
(2)请你求出小明离开学校的路程 ![]() (千米)与所经过的时间
(千米)与所经过的时间 ![]() (分钟)之间的函数表达式;
(分钟)之间的函数表达式;
(3)若设两人在路上相距不超过 ![]() 千米时称为可以“互相望见”,则小聪和小明可以“互相 望见”的时间共有多少分钟?
千米时称为可以“互相望见”,则小聪和小明可以“互相 望见”的时间共有多少分钟?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中.过一点分別作坐标轴的垂线,若与坐标轴围成矩形的周长的数值与面积的数值相等,则这个点叫做和谐点.例如.图中过点P分別作x轴,y轴的垂线.与坐标轴围成矩形OAPB的周长的数值与面积的数值相等,则点P是和谐点. 
(1)判断点M(1,2),N(4,4)是否为和谐点,并说明理由;
(2)若和谐点P(a,3)在直线y=﹣x+b(b为常数)上,求a,b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣ ![]() (x﹣1)2+3与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.
(x﹣1)2+3与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.
(1)如图1.求点A的坐标及线段OC的长;
(2)点P在抛物线上,直线PQ∥BC交x轴于点Q,连接BQ.
①若含45°角的直角三角板如图2所示放置.其中,一个顶点与点C重合,直角顶点D在BQ上,另一个顶点E在PQ上.求直线BQ的函数解析式;
②若含30°角的直角三角板一个顶点与点C重合,直角顶点D在直线BQ上,另一个顶点E在PQ上,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块余料ABCD,AD∥BC,现进行如下操作:以点B为圆心,适当长为半径画弧,分别交BA,BC于点G,H;再分别以点G,H为圆心,大于![]() GH的长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.
GH的长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.
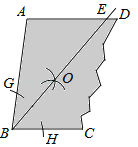
(1)求证:AB=AE;
(2)若∠A=100°,求∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上的一点且GH⊥EG.求证:PF∥GH.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】射线![]() 绕原点
绕原点![]() 从数轴的正半轴逆时针旋转一定的角度
从数轴的正半轴逆时针旋转一定的角度![]() (
(![]() ),射线上的一点
),射线上的一点![]() 与原点
与原点![]() 的距离(
的距离(![]() )为
)为![]() ,并规定:当
,并规定:当![]() 或
或![]() 时,点
时,点![]() 的位置记作
的位置记作![]() ;当
;当![]() 时,点
时,点![]() 的位置记作
的位置记作![]() .如图,点
.如图,点![]() 、
、![]() 的位置表示为
的位置表示为![]() ,
,![]() .回答下列问题:
.回答下列问题:
(1)已知点![]() ,点
,点![]() ,则点
,则点![]() 与点
与点![]() 的距离为 ;线段
的距离为 ;线段![]() 的中点
的中点![]() 的位置是( , ).
的位置是( , ).
(2)已知点![]() ,点
,点![]() ,
,![]() ,点
,点![]() 从
从![]() 点出发,以每秒2个单位长度的速度在线段
点出发,以每秒2个单位长度的速度在线段![]() 上来回运动;同时射线
上来回运动;同时射线![]() 以每秒10°的速度绕原点
以每秒10°的速度绕原点![]() 逆时针旋转,当时间
逆时针旋转,当时间![]() (其中
(其中![]() )为何值时,
)为何值时,![]() ?并求出此时三角形
?并求出此时三角形![]() 的面积.
的面积.
(3)直接写出位置满足![]() 的所有点所围成的图形面积.(结果保留一位小数)
的所有点所围成的图形面积.(结果保留一位小数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,李老师出示了如下框中的题目.

小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况探索结论
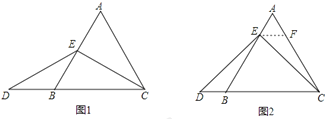
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:AE__________DB(填“>”,“<”或“=”).
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE__________DB(填“>”,“<”或“=”).理由如下:
如图2,过点E作EF∥BC,交AC于点F,(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com