
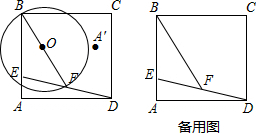
ЗжЮі ЃЈ1ЃЉШчЭМ1ЃЌИљОнЙДЙЩЖЈРэЕУЃКED2=AE2+AD2=a2+102=a2+100ЃЌдкRtЁїBGFжаЃЌгЩЙДЙЩЖЈРэЕУЃКBF2=BG2+GF2ЃЌДњШыПЩЕУНсЙћЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌжЄУїЫФБпаЮBGFHЪЧОиаЮЃЌЕУBH=GF=$\frac{1}{2}$AD=$\frac{1}{2}$BCЃЌЫљвдЁбOБиЙ§BCЕФжаЕуЃЛ
ЃЈ3ЃЉвђЮЊЁбOВЛПЩФмгыБпABКЭBCЯрЧаЃЌЫљвдЗжСНжжЧщПіЃК
ЂйШчЭМ2ЃЌЕБЁбOгыБпCDЯрЧаЪБЃЌИљОнRtЁїONFжаЃЌON2+NF2=OF2=OM2ЃЌСаЪН$ЃЈ\frac{5}{2}ЃЉ^{2}$+ЃЈ$\frac{7}{4}a$ЃЉ2=$ЃЈ\frac{15}{2}ЃЉ^{2}$ЃЌЧѓaЕФжЕЃЛ
ЂкШчЭМ3ЃЌЕБЁбOгыБпADЯрЧаЪБЃЌЩшЧаЕуЮЊQЃЌИљОнЃК$B{F}^{2}=25+\frac{49}{4}{a}^{2}$ ЧвBF=2OQЃЌСаЪНПЩЕУНсТлЃЛ
ЃЈ4ЃЉЗжБ№МЦЫуЕБaзюаЁКЭзюДѓЪБЃЌМДAЁфдкБпBCЩЯКЭБпCDЩЯЃЌзїИЈжњЯпЃЌИљОнЖдГЦЕуЕФСЌЯпБЛЖдГЦжсДЙжБЦНЗжЃЌгЩЯпЖЮДЙжБЦНЗжЯпЕФаджЪСаЪНПЩЕУНсТлЃЎ
НтД№ 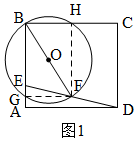 НтЃКЃЈ1ЃЉШчЭМ1ЃЌЁпЫФБпаЮABCDЪЧОиаЮЃЌ
НтЃКЃЈ1ЃЉШчЭМ1ЃЌЁпЫФБпаЮABCDЪЧОиаЮЃЌ
ЁрЁЯA=90ЁуЃЌ
дкRtЁїAEDжаЃЌAE=aЃЌAD=10ЃЌ
гЩЙДЙЩЖЈРэЕУЃКED2=AE2+AD2=a2+102=a2+100ЃЌ
ЩшЁбOНЛABгкGЃЌСЌНгFGЃЌ
ЁпBFЪЧЁбOЕФжБОЖЃЌ
ЁрЁЯBGF=90ЁуЃЌ
ЁпЁЯA=90ЁуЃЌ
ЁрЁЯBGF=ЁЯAЃЌ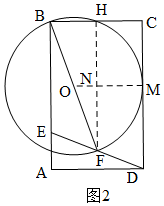
ЁрFGЁЮADЃЌ
ЁпFЪЧEDЕФжаЕуЃЌ
ЁрGF=$\frac{1}{2}$AD=5ЃЌEG=AG=$\frac{1}{2}$aЃЌ
ЁпAE=$\frac{1}{4}$AB=aЃЌ
ЁрAB=4aЃЌ
ЁрBG=4a-$\frac{1}{2}$a=$\frac{7}{2}$aЃЌ
гЩЙДЙЩЖЈРэЕУЃКBF2=BG2+GF2ЃЌ
ЁрBF2=$ЃЈ\frac{7}{2}aЃЉ^{2}$+52=$\frac{49}{4}{a}^{2}$+25=$\frac{49{a}^{2}+100}{4}$ЃЌ
ЙЪД№АИЮЊЃКa2+100ЃЛ$\frac{49{a}^{2}+100}{4}$ЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЩшЁбOНЛBCгкHЃЌСЌНгFHЃЌ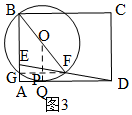
ЁпBFЪЧЁбOЕФжБОЖЃЌ
ЁрЁЯBHF=90ЁуЃЌ
ЁрЁЯABC=ЁЯBHF=ЁЯAGF=90ЁуЃЌ
ЁрЫФБпаЮBGFHЪЧОиаЮЃЌ
ЁрBH=GF=$\frac{1}{2}$AD=$\frac{1}{2}$BCЃЌ
ЁрHЪЧBCЕФжаЕуЃЌ
МДЃКЁбOБиЙ§BCЕФжаЕуЃЛ
ЃЈ3ЃЉЗжСНжжЧщПіЃК
ЂйШчЭМ2ЃЌЕБЁбOгыБпCDЯрЧаЪБЃЌЩшЧаЕуЮЊMЃЌСЌНгOMЁЂFHНЛгкNЃЌдђOMЁЭCDЃЌ
ЁрOM=ON+MN=$\frac{5}{2}$+5=$\frac{15}{2}$ЃЌ
ЁпOMЁЭFHЃЌ
ЁрNF=$\frac{1}{2}$FH=$\frac{1}{2}$ЁС$\frac{7}{2}\\;a$=$\frac{7}{4}$aЃЌ
RtЁїONFжаЃЌON2+NF2=OF2=OM2ЃЌ
Ёр$ЃЈ\frac{5}{2}ЃЉ^{2}$+ЃЈ$\frac{7}{4}a$ЃЉ2=$ЃЈ\frac{15}{2}ЃЉ^{2}$ЃЌ
a=$ЁР\frac{20}{7}$ЃЌ
ЁпaЃО0ЃЌ
Ёрa=$\frac{20}{7}$ЃЌ
ЂкШчЭМ3ЃЌЕБЁбOгыБпADЯрЧаЪБЃЌЩшЧаЕуЮЊQЃЌ
СЌНгOQЃЌдђOQЁЭADЃЌСЌНгFGЃЌНЛOQгкPЃЌ
ЁрOQ=OP+PQ=$\frac{1}{2}$BG+AG=$\frac{7}{4}a$+$\frac{1}{2}a$=$\frac{9}{4}$aЃЌ
гЩЃЈ1ЃЉжЊЃК$B{F}^{2}=25+\frac{49}{4}{a}^{2}$ ЧвBF=2OQЃЌ
Ёр25+$\frac{49}{4}\\;{a}^{2}$a2=ЃЈ2ЁС$\frac{9}{4}$aЃЉ2ЃЌ
a=$\frac{5\sqrt{2}}{4}$ЃЌ
злЩЯЫљЪіЃЌШєЁбOгыОиаЮABCDИїБпЫљдкЕФжБЯпЯрЧаЪБЃЌaЕФжЕЮЊ$\frac{20}{7}$Лђ$\frac{5\sqrt{2}}{4}$ЃЛ
ЃЈ4ЃЉШчЭМ4ЃЌЕБAЕФЖдГЦЕуAЁфЧЁКУдкБпBDЩЯЪБЃЌСЌНгAAЁфНЛBFгкHЃЌСЌНгAFЁЂAЁфFЃЌЙ§FзїMNЁЭBCЃЌНЛBCгкMЃЌНЛADгкNЃЌдђMNЁЭADЃЌ
ЁпAЙигкжБЯпBFЕФЖдГЦЕуAЁфЃЌ
ЁрBFЪЧAAЁфЕФДЙжБЦНЗжЯпЃЌ
ЁрAF=AЁфFЃЌAB=AЁфB=4aЃЌ
гЩЃЈ1ЃЉЃЈ2ЃЉЕУЃКFN=$\frac{1}{2}$aЃЌFM=$\frac{7}{2}$aЃЌAЁфM=4a-5ЃЌAN=5ЃЌ
гЩЙДЙЩЖЈРэЕУЃК${5}^{2}+ЃЈ\frac{1}{2}aЃЉ^{2}$=ЃЈ4a-5ЃЉ2+$ЃЈ\frac{7}{2}aЃЉ^{2}$ЃЌ
НтЕУЃКa1=0ЃЈЩсЃЉЃЌa2=$\frac{10}{7}$ЃЌ
ЁрЕБaЃМ$\frac{10}{7}$ЪБЃЌAЁфТфдкОиаЮABCDЭтВПЃЈАќРЈБпНчЃЉЃЌ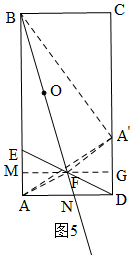
ШчЭМ5ЃЌЕБAЁфТфдкБпCDЩЯЪБЃЌСЌНгAAЁфЁЂAЁфBЃЌЙ§FзїMGЁЭABЃЌдђMGЁЭCDЃЌ
ЩшЩфЯпBFНЛADгкNЃЌ
взЕУAЁфG=AM=DG=$\frac{1}{2}$aЃЌAЁфC=3aЃЌ
ЁпBFЪЧAAЁфЕФДЙжБЦНЗжЯпЃЌ
ЁрAB=AЁфBЃЌ
дђЃЈ4aЃЉ2=102+ЃЈ3aЃЉ2ЃЌ
a=$\frac{10}{7}\sqrt{7}$ЃЌ
ЁрaЕФШЁжЕЗЖЮЇЪЧЃК$\frac{10}{7}$ЃМaЃМ$\frac{10}{7}\sqrt{7}$ЃЌ
ЙЪД№АИЮЊЃК$\frac{10}{7}$ЃМaЃМ$\frac{10}{7}\sqrt{7}$ЃЎ
ЕуЦР БОЬтЪЧдВКЭЫФБпаЮЕФзлКЯЬтЃЌПМВщСЫШ§НЧаЮжаЮЛЯпЖЈРэЁЂЯпЖЮДЙжБЦНЗжЯпаджЪЁЂЖдГЦЕФаджЪЁЂЙДЙЩЖЈРэЁЂОиаЮЕФаджЪЃЌЕкШ§ЮЪКЭЕкЫФЮЪжаВЩгУЗжРрЬжТлЕФЫМЯыЃЌзЂвтВЛвЊЖЊНтЃЌЕкЫФЮЪгаФбЖШЃЌзМШЗЛГіЭМаЮЪЧЙиМќЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
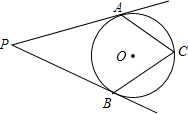 ШчЭМЃЌPAЃЌPBЪЧЁбOЕФЧаЯпЃЌЧаЕуЗжБ№ЮЊAЃЌBЃЌCдкЁбOЩЯЃЌдђЁЯPгыЁЯCЕФЙиЯЕЪЧЃЈЁЁЁЁЃЉ
ШчЭМЃЌPAЃЌPBЪЧЁбOЕФЧаЯпЃЌЧаЕуЗжБ№ЮЊAЃЌBЃЌCдкЁбOЩЯЃЌдђЁЯPгыЁЯCЕФЙиЯЕЪЧЃЈЁЁЁЁЃЉ| AЃЎ | 2ЁЯP+ЁЯC=180Ёу | BЃЎ | 2ЁЯP+ЁЯC=360Ёу | CЃЎ | ЁЯP+2ЁЯC=180Ёу | DЃЎ | ЁЯP+ЁЯC=180Ёу |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
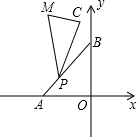 ШчЭМЃЌAЃЈ-3ЃЌ0ЃЉЃЌBЃЈ0ЃЌ3ЃЉЃЌCЃЈ-1ЃЌ4ЃЉЃЌPЃЌCЃЌMАДФцЪБеыЫГађХХСаЃЌЖЏЕуPдкЯпЖЮABЩЯЃЌЁЯC=90ЁуЃЌЁЯCPM=30ЁуЃЌЧыЧѓГіЕБPЕуДгAдЫЖЏЕНBЕуЪБЃЌЕуMдЫЖЏЕФТЗОЖЪБЪВУДЃПВЂЧѓГіMЕудЫЖЏТЗОЖГЄЖШЃЎ
ШчЭМЃЌAЃЈ-3ЃЌ0ЃЉЃЌBЃЈ0ЃЌ3ЃЉЃЌCЃЈ-1ЃЌ4ЃЉЃЌPЃЌCЃЌMАДФцЪБеыЫГађХХСаЃЌЖЏЕуPдкЯпЖЮABЩЯЃЌЁЯC=90ЁуЃЌЁЯCPM=30ЁуЃЌЧыЧѓГіЕБPЕуДгAдЫЖЏЕНBЕуЪБЃЌЕуMдЫЖЏЕФТЗОЖЪБЪВУДЃПВЂЧѓГіMЕудЫЖЏТЗОЖГЄЖШЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
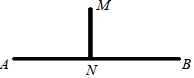 ШчЭМЫљЪОЃЌАбКгЫЎв§ЯђЫЎГиMЃЌвЊЯђЫЎГиMЕуЯђКгАЖABЛДЙЯпЃЌДЙзуЮЊNЃЌдйбиДЙЯпMNПЊвЛЬѕЧўЕРВХФмЪЙЧўЕРзюЖЬЃЎЦфвРОнЪЧЃЈЁЁЁЁЃЉ
ШчЭМЫљЪОЃЌАбКгЫЎв§ЯђЫЎГиMЃЌвЊЯђЫЎГиMЕуЯђКгАЖABЛДЙЯпЃЌДЙзуЮЊNЃЌдйбиДЙЯпMNПЊвЛЬѕЧўЕРВХФмЪЙЧўЕРзюЖЬЃЎЦфвРОнЪЧЃЈЁЁЁЁЃЉ| AЃЎ | ДЙЯпЖЮзюЖЬ | |
| BЃЎ | Й§вЛЕуШЗЖЈвЛЬѕжБЯпгывбжЊжБЯпДЙжБ | |
| CЃЎ | СНЕужЎМфЯпЖЮзюЖЬ | |
| DЃЎ | вдЩЯЫЕЗЈЖМВЛЖд |
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com