
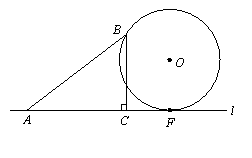
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,边AC在直线l上,点F是直线l上的一个动点,过点B的⊙O与直线l相切于点F.设CF=x,⊙O的半径为y.
(1)用x的代数式表示y;
(2)点F在运动的过程中,是否存在这样的x, 使⊙O与△ABC的两边所在直线同时相切?若存在,求出x的值;若不存在,请说明理由.
科目:初中数学 来源: 题型:
已知:图1是一块学生用直角三角板,其中∠A′=30°,三角板的边框为透明塑料制成(内、外直角三角形对应边互相平行且三处所示宽度相等).将直径为4cm的⊙O移向三角板,三角板的内ABC的斜边AB恰好等于⊙O的直径,它的外△A′B′C′的直角边A′C′ 恰好与⊙O相切(如图2),则边B′C′的长为 cm.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
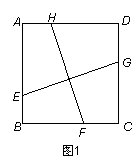
如图1,已知正方形ABCD ,点E、F、G、H分别在边AB、BC、CD、DA上,若EG⊥FH,则易证: EG = FH .
(1)如果把条件中的“正方形”改为“长方形”,并设AB=2,BC=3(如图2),试探究EG、FH之间有怎样的数量关系,并证明你的结论;
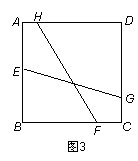
(2)如果把条件中的 “EG⊥FH” 改为 “EG与FH的夹角为45°”,并假设正方形ABCD的边长为1,FH 的长为  (如图3),试求EG的长度.
(如图3),试求EG的长度.
 |  | ||||
 | |||||
查看答案和解析>>
科目:初中数学 来源: 题型:
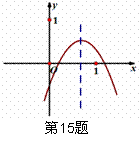
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则在下列代数式①ac,②a+b+c,
③4a-2b+c,④2a+b,⑤b2-4ac中,值大于0的序号为__ __.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
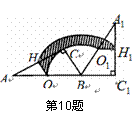
如图,Rt△ABC中,∠ACB=90°,∠CAB=30°,BC=2,O、H分别为边AB、AC的中点,将△ABC绕点B顺时针旋转120°到△A1BC1的位置,则整个旋转过程中线段OH所扫过部分的面积(即阴影部分面积)为 ( )
A.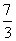 π-
π-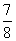
 B.
B.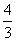 π+
π+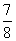
 C.π D.
C.π D.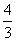 π+
π+
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
某化工材料经销公司购进了一种化工原料共7 000 kg,购进价格为每千克30元,物价部门规定其销售单价不得高于每千克70元,也不得低于30元.市场调查发现:单价定为70元时,日均销售60 kg;单价每降低1元,日均多售出2 kg,在销售过程中,每天还要除去其他费用400元(天数不足一天时,按整天计算) .设销售单价为x元,日均获利为y元. (日均获利=销售所得利润-各种开支)
(1) 求y关于x的函数关系式,并写出x的取值范围;
(2) 求每千克单价定为多少元时日均获利最多,是多少?
(3) 若用日均获利最多的方式销售或按销售单价最高销售,试比较哪一种销售获总利更多,多多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com