
 如图,已知点O(0,0),A(2,1),抛物线l:y=-(x-h)2+1(h为常数)与y轴的交点为B.
如图,已知点O(0,0),A(2,1),抛物线l:y=-(x-h)2+1(h为常数)与y轴的交点为B.分析 ,(1)把A(2,1)代入二次函数的解析式计算,得到解析式,根据二次函数的性质得到抛物线l的对称轴及顶点坐标;
(2)根据坐标的特征求出yB,根据平方的非负性求出yB的最大值,根据二次函数的性质比较y1与y2的大小即可.
解答 解:(1)把A(2,1)代入y=-(x-h)2+1,
得:-(2-h)2+1=1,
解得:h=2,
∴解析式为:y=-(x-2)2+1,
∴对称轴为:x=2,顶点坐标为:(2,1);
(2)点B的横坐标为0,则yB=-h2+1,
∴当h=0时,yB有最大值为1,
此时,抛物线为:y=-x2+1,对称轴为y轴,
当x≥0时,y随着x的增大而减小,
∴x1>x2≥0时,y1<y2.
点评 本题考查的是二次函数的最值的确定、待定系数法的应用,灵活运用待定系数法求出二次函数的解析式、熟记二次函数的性质是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图,这是某市部分简图(图中小正方形的边长代表1km长).以火车站为坐标原点建立平面直角坐标系.
如图,这是某市部分简图(图中小正方形的边长代表1km长).以火车站为坐标原点建立平面直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
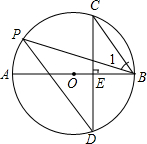 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C.
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com